4.02. Дифференциал функции

Определение 1. Функция называется Дифференци-руемой в точке , если ее приращение в этой точке представимо в виде

. (1)

Определение 2. Линейная функция от переменной называется Дифференциалом функции в точке и обозначается или

= . (2)

Подставляя это выражение в формулу (1), получим связь приращения дифференцируемой функции с ее дифференциалом

. (3)

Приращение функции отличается от дифференциала на бесконечно малую.

Для симметрии записи (2) величину обозначают и называют Дифференциалом независимого Аргумента. Тогда, , и как будет показано ниже, . Окончательно,

. (4)

Пример 1. Найти дифференциал функции .

Для этого выделим линейную (по ) часть приращения

.

Теорема 1. Функция дифференцируема в точке тогда и только тогда, когда существует производная в точке .

Необходимость. Пусть функция дифференцируема в точке , тогда в точке приращение представимо виде . Переходя к пределу в этом равенстве, получим . Отсюда следует, что предел существует и по определению производной .

Достаточность. Пусть существует производная . Тогда

где

Т. е. функция дифференцируема в точке .

Теорема 2. Если функция дифференцируема в некото-рой точке , то она непрерывна в этой точке.

Доказательство. Пусть функция дифференцируема в точке , тогда

,

Т. е. функция непрерывна в точке .

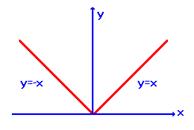
Замечание. Обратно утверждение теоремы, вообще говоря, неверно, т. е. из непрерывности функции не следует ее дифференцируемость. Например, функция непрерывна в точке , но не имеет производной в этой точке, т. е. не дифференцируема в точке :

Т. е. функция непрерывная в точке , но

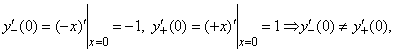т. е. не имеет производной в точке .

< Предыдущая		Следующая >