4.01. Производная. Определение производной
Во многих прикладных задачах интересует не значение функции в точке, а ее изменение на некотором промежутке. Например, при деформации пружины интересует, не ее длина, а величина ее деформации; не значение энергии системы, а работа системы как изменение ее энергии, и т. д.
Возьмем две произвольные точки на оси ![]() , или говорят, два значения независимой переменной
, или говорят, два значения независимой переменной ![]() и
и ![]() . Обозначим
. Обозначим ![]() . Величина
. Величина ![]() называется Прираще-нием Независимой переменной (или Независимого аргумента) в точке
называется Прираще-нием Независимой переменной (или Независимого аргумента) в точке ![]() . Аналогично, для функции
. Аналогично, для функции ![]() имеем значения:
имеем значения: ![]() и
и ![]() . Вели-чина
. Вели-чина ![]() называется Приращением зависимой переменной (или Приращением функции) в точке
называется Приращением зависимой переменной (или Приращением функции) в точке ![]() .
.
Определение 1. Если в точке ![]() существует предел (конечный или бесконечный)
существует предел (конечный или бесконечный)
![]() , (1)
, (1)
То этот предел называется Производной функции ![]() в точке
в точке ![]() . Обозначается:
. Обозначается: 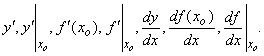
Замечание. Если ![]() - произвольная точка множества
- произвольная точка множества ![]() , то
, то ![]() (
(![]() ) является функцией
) является функцией ![]() на множестве
на множестве ![]() . В этом случае
. В этом случае ![]() обозначают
обозначают ![]() и
и ![]() (
(![]() ) рассматривается как функция от пере-менной
) рассматривается как функция от пере-менной ![]() .
.
Определение 2. Если существует предел (1) функции ![]() слева (справа) в точке
слева (справа) в точке ![]() , то этот предел называется производной слева (справа) в точке
, то этот предел называется производной слева (справа) в точке ![]() и обозначается
и обозначается ![]()
![]() .
.
Теорема. Функция ![]() имеет производную в точке
имеет производную в точке ![]() тогда и только тогда, когда существуют односторонние производные и они равны
тогда и только тогда, когда существуют односторонние производные и они равны ![]() .
.
Операция вычисления производной от функции в некоторой точке называется Дифференцированием Функции в этой точке.
Таблица производных
Выводится по определению производной ![]() .
.
1. ![]() ,
, ![]() .
.
![]() .
.
2. ![]() .
.

3. ![]() .
.
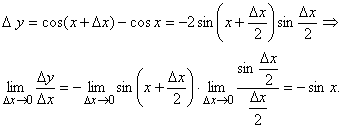
4. ![]() .
.
![]() 5.
5. ![]() .
.
Следует из предыдущей формулы при ![]() .
.
6. ![]() ,
, ![]() .
.
Применим формулу бинома Ньютона
![]()

Формула (6) оказывается справедливой не только для целых ![]() , но для действительных значений степени.
, но для действительных значений степени.
| < Предыдущая | Следующая > |
|---|