3.3. Метод выделения главной части функции

Определение 1. Функция называется Малой более высокого Порядка по сравнению с функцией при , если и и обозначается .

Примеры. 1. при , т. к. . Заметим, что при : ~, . Число назы-вается Порядком малости функции .

Определение 2. Функция называется Большой более высокого Порядка по сравнению с функцией при , если и .

2. при , т. к. .

Определение 3. Функция называется Главной частью функции при , если она представима при в виде .

При этом, функции и называются Эквивалент-ными при и обозначаются ~ .

Теорема 1. Для того чтобы функции и были экви-валентными при необходимо и достаточно, чтобы

=1.

Теорема 2. Следующие функции эквивалентными между собой при

~ ~ ~ ~ ~ .

Первые три соотношения следуют из 1-го замечательного предела и его следствий, а четвертое и пятое - из следствий 2-го замечательного предела.

Теорема 3. ~ при .

Применим первый замечательный предел и формулу бинома Ньютона к тождеству

~ ~ при .

Выделение главной части функции значительно упрощает вычисление пределов.

Примеры.

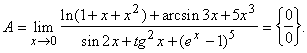
Поскольку ~ , ~ , ~ , ~ ~ , ~ , то . Наконец, ~ , ~ при , то

Т. к. ~, ~ 3, то .

3. .

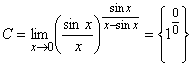Здесь нельзя использовать эквивалентные функции: ~, т. к. получим неопределенность. Преобразуем основание степени

Тогда,

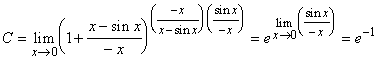Замечание. Последний пример продемонстрировал, что методом выделения главной части функции следует обращаться осторожно. Может оказаться, что решающую роль играет не главная часть функции, а другие ее части.

< Предыдущая		Следующая >