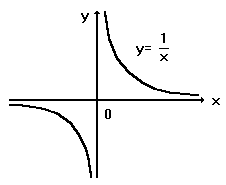3.2. Классификация точек разрыва функции

Определение 1. Точка называется Точкой разрыва функции , если она не определена в точке , или, если она определена точке , но не является в ней непрерывной.

Разрыв 1-го рода. Точка называется точкой разрыва 1-го ро-да функции , если существуют конечные односторонние пределы , , но .

Величина - называется Скачком функции в точке .

Пример. Функция 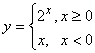имеет точку разрыва 1-го рода в точке , т. к. , и скачок равен .

Устранимый разрыв. Точка называется точкой устранимого разрыва функции , если существуют конечные и равные между собой односторонние пределы = , но функция не определена в точке .

В этом случае можно доопределить функцию в точке , положив == .

Пример. Функция имеет разрыв в точке , т. к. она не определена в этой точке, но . Устраним разрыв, положив , т. е.

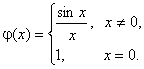
Теперь функция непрерывна в точке .

Разрыв 2-го рода. Точка называется точкой разрыва 2-го рода функции , если не существует или является бесконечным хотя бы один из односторонних пределов или .

Примеры.

1. Функция имеет разрыв 2-го рода в точке , т. к. .

2. Функция имеет разрыв 2-го рода в точке , т. к. не существует предел .

< Предыдущая		Следующая >