3.1. Непрерывность функции. Понятие непрерывности функции. Свойства непрерывных функций
Определение 1. Функция ![]() называется Непрерывной в точке
называется Непрерывной в точке ![]() , если она определена в точке
, если она определена в точке ![]() и существует предел
и существует предел ![]() .
.
Теорема 1. Для того чтобы функция ![]() имела конечный предел в точке
имела конечный предел в точке ![]() необходимо и достаточно, чтобы она была непрерывной в этой точке.
необходимо и достаточно, чтобы она была непрерывной в этой точке.
Необходимость. Пусть ![]() , тогда
, тогда ![]() имеем
имеем ![]() . Полагая
. Полагая ![]() имеем
имеем ![]() , т. е.
, т. е. ![]() , следовательно, функция
, следовательно, функция ![]() непрерывна.
непрерывна.
Достаточность. Пусть ![]() . Тогда, полагая
. Тогда, полагая ![]() , получим
, получим ![]() , т. е.
, т. е. ![]()
![]() .
.
Замечание. По определению в точке ![]() функция не является непрерывной.
функция не является непрерывной.
Определение 2. Функция ![]() называется Непрерывной слева (Справа) в точке
называется Непрерывной слева (Справа) в точке ![]() , если
, если
![]()
![]() .
.
Теорема 2. Для того чтобы функция ![]() была непрерывной в точке
была непрерывной в точке ![]() необходимо и достаточно, чтобы выполнялись равенства
необходимо и достаточно, чтобы выполнялись равенства
![]() .
.
Пример. Функция

Непрерывна в точке ![]() , т. к.
, т. к.
![]() Имеют место равенства
Имеют место равенства ![]() .
.
Свойства непрерывных функций аналогичные свойствам пределов функций. Следует только значения пределов ![]() и
и ![]() функций
функций ![]() и
и ![]() в точке
в точке ![]() заменить значениями
заменить значениями ![]() и
и ![]() . Доказательства этих свойств проводится аналогично как для пределов функций.
. Доказательства этих свойств проводится аналогично как для пределов функций.
Формы записи непрерывности:
|
1. По определению |
|
|
2. По Гейне |
|
|
3. По Коши |
|
|
4. В терминах приращений |
|
Последнее определение следует из первого
![]() ,
,
Где ![]() - называется Приращением функции
- называется Приращением функции ![]() в точке
в точке ![]() ,
, ![]() - Приращением аргумента
- Приращением аргумента ![]() в точке
в точке ![]() .
.
Теорема 3. Основные элементарные функции непрерывны во всех точках определения этих функций.
В качестве примера рассмотрим только две элементарные функции. Так, функция ![]() непрерывна на всей числовой оси, кроме точки
непрерывна на всей числовой оси, кроме точки ![]() , т. к.
, т. к.![]()
![]() имеем
имеем
![]() .
.
Функция ![]() непрерывна на всей числовой оси, т. к.
непрерывна на всей числовой оси, т. к. ![]() имеем
имеем
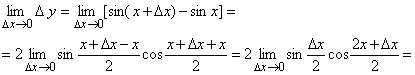
![]() .
.
Аналогично доказывается непрерывность остальных элемен-тарных функций.
| < Предыдущая | Следующая > |
|---|