2.3. Второй замечательный предел

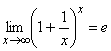
Второй замечательный предел имеет неопределенность .

Рассмотрим последовательность Применим формулу бинома Ньютона

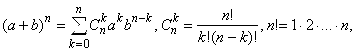
Получим

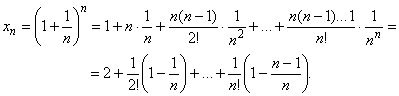
Перейдем от к , тогда число положительных слагаемых увеличится и, кроме того, -е слагаемое больше -го последовательности , т. к. . Поэтому , т. е. последовательность монотонно возрастающая, кроме того, она ограничена, т. к.

.

Откуда следует .

Итак, последовательность возрастает и ограничена сверху, следовательно, имеет предел, который обозначается . Более точные расчеты показывают, что число иррациональное и ее приближенное значение равно

Следствие 1.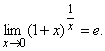

В исходной формуле 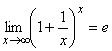сделаем замену , тогда, при имеем и

Следствие 2.

Первая формула следует из

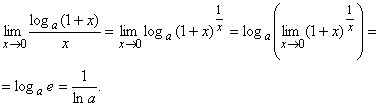
Вторая формула следует из первой при .

Следствие 3.

Вторая формула следует из первой при , а для доказательства первой сделаем замену переменной . Тогда, при имеем и . Поэтому

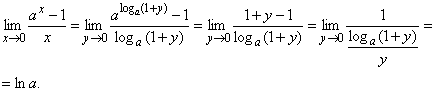
Примеры:

1.

2.

3.

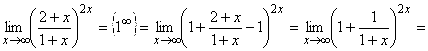
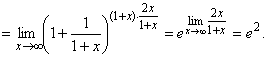
Перед вычислением предела следует проверить наличие неопределенности, ее может не быть.

4.

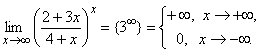
< Предыдущая		Следующая >