1.09. Бесконечно малые и бесконечно большие функции

Определение 1. Функция называется Бесконечно малой (Б/м) при , если .

Примеры Б/м:

при

при .

Как видно из примеров понятие Б/м относительное, так, при имеем уже не есть Б/м.

Теорема 1. Для того чтобы существовал предел , необходимо и достаточно, чтобы , где есть Б/м при .

Краткая запись: , .

Необходимость. Пусть . Положим . По определению предела в окрестности

,

Т. е. есть Б/м при . Отсюда следует, что .

Достаточность. Пусть и . Тогда,

.

Cвойства б/м:

Сумма конечного числа Б/м есть Б/м;

Произведение конечного числа Б/м есть Б/м;

Произведение Б/м на ограниченную функ-цию есть Б/м.

Докажем теорему для суммы двух Б/м, т. е.. По определению Б/м

и .

Тогда .

Для произведения следует положить и , а для произведения Б/м на ограниченную функцию - положить .

В качестве приложения свойств Б/м докажем свойство 5 пределов функций. Начнем с предела произведения функций . Положим , где и есть Б/м при . Тогда

По свойствам Б/м последние три слагаемые есть Б/м. Поэтому

.

Аналогично доказывается формула для предела частного функций:

т. е. ,

Где есть Б/м.

Следовательно, = .

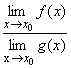Определение 2. Функция Называется Бесконечно большой (Б/б) при , если .

Примеры Б/б:

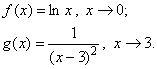
Теорема 2. Если функция есть Б/б при , то функция есть Б/м при , и наоборот, если функция есть Б/м при и , то функция есть Б/б.

Докажем только первое утверждение. Пусть . По определению , т. е. , отсюда следует, что функция есть Б/м.

Исходя из свойств Б/м и Б/б вводят символические обозначе-ния для :

.

Пример.

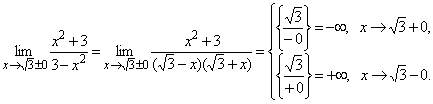
< Предыдущая		Следующая >