1.10*. Предел последовательности множеств
Обобщим определение предела на множества произвольной природы. Заметим сразу, что, если ![]() - монотонно убывающая последовательность множеств, т. е. такая, что
- монотонно убывающая последовательность множеств, т. е. такая, что ![]() , то
, то ![]() . Если
. Если ![]() - монотонно возрастающая после-довательность, то
- монотонно возрастающая после-довательность, то ![]() .
.
В произвольном случае, пусть ![]() - Бесконечная последо-вательность множеств. Обозначим
- Бесконечная последо-вательность множеств. Обозначим
![]() ,
, ![]() .
.
Множество ![]() Можно интерпретировать, как все члены после-довательности
Можно интерпретировать, как все члены после-довательности ![]() , а
, а ![]() - только, начиная с некоторого номера. Очевидно,
- только, начиная с некоторого номера. Очевидно, ![]() . Множество
. Множество ![]() Называется Верхним Пределом, а
Называется Верхним Пределом, а ![]() - Нижним пределом последовательности множеств
- Нижним пределом последовательности множеств ![]() и обозначаются
и обозначаются ![]() ,
, ![]() .
.
Очевидно, что у последовательности множеств ![]() существует предел
существует предел ![]() , если
, если ![]() или
или ![]() .
.
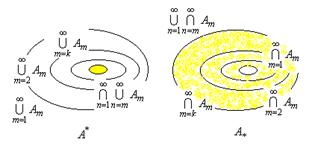
Определение предела последовательности множеств ![]() .
.
Предел последовательности множеств ![]() произвольной природы можно определить так:
произвольной природы можно определить так: ![]() , где
, где ![]() - Для
- Для ![]() выполнено неравенство
выполнено неравенство ![]() ;
; ![]() - Существует такое
- Существует такое ![]() , что неравен-ство выполняется при
, что неравен-ство выполняется при ![]() ;
; ![]() - для всех K Существует такое N, Что при
- для всех K Существует такое N, Что при ![]() выполнено неравенство
выполнено неравенство ![]() .
.
| < Предыдущая | Следующая > |
|---|