1.07. Свойства пределов функций

Первые шесть свойств формулируются и доказываются аналогично как для последовательностей. Следует только заменить на ; на ; на .

1. Единственность предела. Функция может иметь только один предел (конечный или определенного знака бесконечный Или ).

2. Предел постоянной. , .

3. «Теорема о двух милиционерах».

Если и , то .

4. Если , и , то

.

Следствие. Если , , и

, то .

5. Арифметические операции над пределами.

Если , , то (), причем

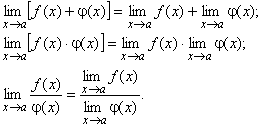
6. Ограниченность предела. Если , то , т. е. функция ограничена.

7. Предел сложной функции.

Если функция определена на , а на и и , то , причем .

Доказательство.

Зафиксируем , тогда . Для , а так как , то . Поскольку выбор произвольный, то .

Примеры:

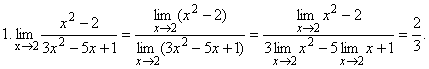
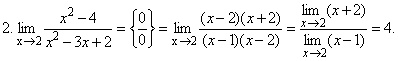
3.,

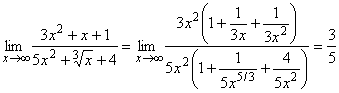Поскольку

Правило. При вычислении пределов от дроби (рациональной или иррациональной), когда аргумент стремится к (, следует вынести в числителе и знаменателе наибольшую степень переменной.

4.

< Предыдущая		Следующая >