1.04. Числовая последовательность и ее предел

Определение 1. Пусть - произвольное множество действитель-ных чисел, а - множество натуральных чисел. Функция называется Числовой последовательностью и обоз-начается . Другими словами, если каждому натуральному числу по некоторому закону ставится в соответствие Единственное действительное число из множества , то говорят, что на множестве определена числовая последова-тельность.

Числа - называются Членами Последователь-ности, - номер члена последовательности .

Примеры: 4 основных вида числовых последовательностей

- монотонно убывающая последователь-ность, для которой выполняется условие .

- монотонно возрастающая пос-ледовательность, для которой выполняется условие .

- ограниченная последователь-ность, для которой существует такое число , что выполняется условие . В данном примере .

- неограниченная последовательность, для которой , что : .

Определение 2. Число называется Пределом последователь-ности , если для любого сколь угодно малого положи-тельного числа существует номер последовательности , зависящий от , такой, что для всех выполняется неравен-ство . Обозначается: .

В логической символике это определение выглядит так:

Обобщим определение на случай, когда является той или иной бесконечно удаленной точкой:

Геометрическая интерпретация предела последовательнос-ти.

Раскрывая в неравенстве модуль, можно запи-сать его в виде . Обозначим этот интервал , который называется Окрестностью Точки . Тогда предел означает, что для фиксиро-ванного все члены последовательности , начиная с некоторго номера : , будут находиться в Окрестности точки . Причем это свойство сохраняется , т. е. при изменении числа (например, при его уменьшении) изменится номер (он возрастет), но свойство сохранится:

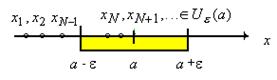
Замечание. Вне окрестности находится конечное число членов последовательности, например, для монотонно возрастающей последовательности - это ее первые членов .

Примеры:

1. В самом деле, возьмем , тогда имеем .

2. Не существует предел .

Запишем подробнее последовательность Она ограничена. Отсюда следует, что предполагаемый ее предел А может находиться между числами и 1. Возьмем , тогда , например, , вне окрестности находится бесконечное число членов последовательности. Это означает, что число А не может быть пределом.

3. .

В самом деле, т. к. , а , то и предел от выражения равен нулю.

Замечание. Решение второй задачи проще осуществить, используя понятие Подпоследовательности , где (бесконечное) подмножество множества . Например, - нечетные или четные натуральные числа. В примере 2 можно выделить, например, две подпоследовательности : и : По определению подпос-ледовательности, ясно, что Предел последовательности сущест-вует, если любая ее подпоследовательность сходится к одному и тому же числу. В примере две подпоследовательности имеют различные значения пределов и . Отсюда следует, что у исходной последовательности нет предела.

< Предыдущая		Следующая >