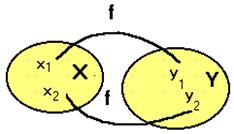
1.02. Понятие функции. Способы их задания
1. Определения и обозначения.
Определение 1. Пусть заданы числовые множества ![]() и
и ![]() . Если каждому элементу
. Если каждому элементу ![]() поставлен в соответствие Единственный элемент
поставлен в соответствие Единственный элемент ![]() по некоторому закону
по некоторому закону ![]() , то говорят, что на множестве
, то говорят, что на множестве ![]() определена (задана) числовая функция
определена (задана) числовая функция ![]() с множеством значений
с множеством значений ![]() .
.
|
|
Обозначают: ![]() ,
, ![]() или
или ![]()
Множество ![]() называют Областью определения функции
называют Областью определения функции ![]() , а
, а ![]() - Множеством Ее Значений.
- Множеством Ее Значений.
Над числовыми функциями производятся Арифметические Операции, т. е. действия как над числами: для функций ![]() ,
, ![]() ,
, ![]() и произвольного числа
и произвольного числа ![]() на множестве
на множестве ![]() определены функции
определены функции ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() .
.
2. Способы задания функции
Аналитический способ.
Функция ![]() задается формулой на множестве
задается формулой на множестве ![]() , на котором эта формула имеет смысл. Например,
, на котором эта формула имеет смысл. Например,
![]() ,
, ![]() ,
, 
Здесь ![]() :
: ![]()
![]() .
.
Графический способ.
Функция ![]() задается точками
задается точками ![]() плоскости
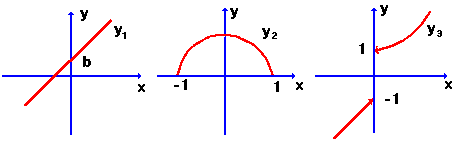
плоскости ![]() . Например, функции предыдущего примера имеют вид
. Например, функции предыдущего примера имеют вид
![]()
Табличный способ.
Функция ![]() задается в виде таблицы ее значений
задается в виде таблицы ее значений
|
|
|
|
. . . |
|
|
|
|
|
. . . |
|
Примерами являются логарифмические, тригонометрические и др. таблицы.
Выделяют специальные аналитические способы задания функций:
1. Неявные функции.
Пусть дано уравнение ![]() . Если
. Если ![]()
![]() , то говорят, что на множестве
, то говорят, что на множестве ![]() определена Неявная Функция
определена Неявная Функция ![]() уравнением
уравнением ![]() .
.
Например, ![]() - неявная функция, хотя, решая уравнение относительно
- неявная функция, хотя, решая уравнение относительно ![]() , получим явную функцию, состоящую из двух ветвей
, получим явную функцию, состоящую из двух ветвей ![]() .
.
В другом примере, ![]() - неявная функция, здесь нельзя выразить явно зависимость
- неявная функция, здесь нельзя выразить явно зависимость ![]() от
от ![]() .
.
2. Сложные функции.
Пусть определены функции ![]() на
на ![]() , а
, а ![]() на
на ![]() . Тогда, если
. Тогда, если ![]() , то говорят, что на
, то говорят, что на ![]() определена Сложная Функция
определена Сложная Функция ![]() , или говорят, Композиция функций
, или говорят, Композиция функций ![]() . Например, если
. Например, если ![]() , то
, то ![]() ; более сложный пример,
; более сложный пример, ![]()
![]()
![]() , тогда
, тогда ![]() .
.
Последние примеры важны при изучении техники диф-ференцирования.
| < Предыдущая | Следующая > |
|---|