2.4. Каноническое уравнение прямой в пространстве
Пусть в пространстве ![]() задана произвольная прямая
задана произвольная прямая ![]() и фиксирована декартова система координат. Возьмем на прямой произвольный вектор
и фиксирована декартова система координат. Возьмем на прямой произвольный вектор ![]() . Его называют Направляющим Вектором Прямой. На этой прямой возьмем две точки - фиксированную
. Его называют Направляющим Вектором Прямой. На этой прямой возьмем две точки - фиксированную ![]() и произвольную
и произвольную ![]() и построим вектор
и построим вектор ![]() .
.
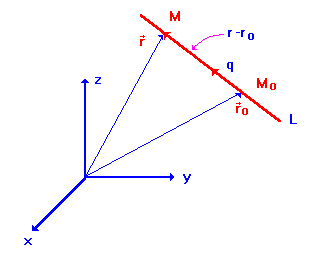
Заметим, что ![]() , поэтому
, поэтому
![]() (1)
(1)
Или в координатах
 .
.
Откуда следует
![]() (2)
(2)
Уравнение (1) называется Векторным уравнением прямой ![]() , а (2) - Каноническими уравнениями прямой
, а (2) - Каноническими уравнениями прямой ![]() , проходящей через точку
, проходящей через точку ![]() с направляющим вектором
с направляющим вектором ![]() .
.
Замечание. В канонических уравнениях прямой (2) одно и / или два из чисел ![]() могут быть равны нулю. Под пропорцией, например,
могут быть равны нулю. Под пропорцией, например, ![]() будем понимать равенство
будем понимать равенство ![]() . Поэтому равенство нулю, например, коэффициента L означает, что
. Поэтому равенство нулю, например, коэффициента L означает, что ![]() .
.
| < Предыдущая | Следующая > |
|---|