7.7. Функциональные ряды (общие положения)

Определение 1. Ряд вида

, (2.1)

Слагаемыми которого являются функции, называется функциональным.

Если зафиксировать аргумент X, то каждая функция станет числом, а ряд (2.1) станет числовым рядом. При одних значениях X этот ряд может оказаться сходящимся, при других – расходящимся.

Определение 2. Областью сходимости Функционального ряда (2.1) называется множество всех тех значений X, при которых ряд сходится. Остальные значения X составляют его область расходимости.

Нас, естественно, в первую очередь будут интересовать области сходимости функциональных рядов, а также суммы рядов в их областях сходимости.

Пусть D – область сходимости данного функционального ряда (2.1). На практике область D может выглядеть по-разному: быть промежутком или интервалом оси Ox, представлять собой всю ось Ox или единственную ее точку, даже быть пустым множеством (последний случай – неинтересный). Для каждого X є D этот ряд имеет конечную сумму S=F(X):

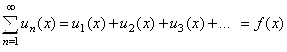(X є D) (2.2)

При исследовании любого функционального ряда встают две основные задачи:

1) Определение его области сходимости D.

2) Определение его суммы F(X) для (X є D). (2.3)

Не менее интересна и обратная проблема: подобрать такой функциональный ряд из возможно более простых слагаемых Un(X), Чтобы он в своей области сходимости D имел сумму, совпадающую с заданной функцией F(X) (то есть чтобы выполнялось равенство (2.2)). Эта проблема называется проблемой разложения заданной функции F(X) в функциональный ряд. Качество решения этой проблемы будет тем выше, чем проще подберется этот ряд; чем быстрее он будет сходиться; тем шире будет его область сходимости D.

Важность решения этой проблемы очень велика. Ведь разлагаемая в функциональный ряд (2.2) функция F(X) может быть сложной и даже не выразимой через элементарные функции. Например, она может быть первообразной для некоторой функции G(X), для которой неопределенный интеграл

Является неберущимся. А слагаемые Un(X) Функционального ряда (2.2), сумма которого будет равна F(X), могут, наоборот, оказаться достаточно простыми элементарными функциями, легко анализируемыми и вычисляемыми. Поэтому получив разложение

(X є D) (2.4)

Нужной нам функции F(X) в такой функциональный ряд, мы в итоге получим возможность для X є D оперировать не с самой функцией F(X), а с ее составляющими U1(X), U2(X), …, которые и проще, и удобнее самой функции.

В следующем параграфе задачи (2.3) и (2.4) будут рассмотрены для двух наиболее простых и важных типов функциональных рядов:

1) Для степенных рядов вида

(2.5)

2) Для обобщенных степенных рядов вида

(2.6)

< Предыдущая		Следующая >