5.06. Интегрирование с помощью подстановки

С помощью замены переменной интегрирования

Суть этого метода в следующем. Пусть требуется вычислить некоторый неопределенный интеграл Нередко его можно упростить, сведя к табличному, путем замены переменной интегрирования Х На какую-то новую переменную (на переменную T), используя подходящую подстановку X = , где - некоторая дифференцируемая функция. Тогда получим следующую Схему вычисления неопределенного интеграла С помощью подстановки:

==== ===

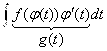Естественно, что применяемая подстановка будет оправданной лишь в том случае, если полученный в результате ее применения интеграл будет проще, чем исходный интеграл .

Примечание. В практических случаях чаще удобнее делать не подстановку вида , а подстановку вида .

Пример 3. Вычислить .

Решение:

==

===

=

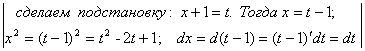Пример 4. Вычислить .

Решение:

= =.

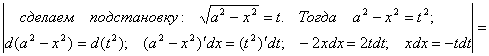Пример 5. Вычислить .

Решение:

== = =.

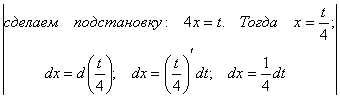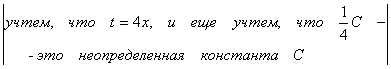
Пример 6. Вычислить .

Решение:

== =

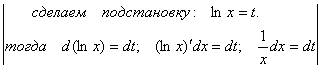Пример 7. Вычислить .

Решение:

=

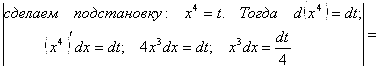
< Предыдущая		Следующая >