5.03. Таблица основных неопределенных интервалов

1. 8.=

2.==X+C 9.= -

3.=+C (N-1) 10.=

4.= 11.= (1.11)

5.=+C 12.= +C

5*.Ex+C 13.=+C

6.= 14.=+C

7.= - 15.=+C

Используя проверку (1.4) для неопределенного интеграла (1.3), легко убедиться в истинности каждого из результатов таблицы (1.11). Проверим, например, первые четыре неопределенные интеграла.

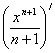1) – Верно; 2) - Верно; 3) = - верно;

4а) Если то и (4) принимает вид: . А это верно, так как

4б) Если то , и (4) принимает вид: . А это верно, так как .

Совершенно аналогично дифференцированием правой части можно подтвердить и все остальные равенства в таблице (1.11).

Таблица (1.11) содержит лишь наиболее простые неопределенные интегралы. Но в математических справочниках содержатся многие сотни (и даже тысячи) наиболее часто встречающихся на практике неопределенных интегралов. К таким справочникам относятся, например, следующие:

1.Бронштейн И. Н. и Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. М., «Наука», 1981.

2.Двайт Г. Б. Таблицы интегралов и другие математические формулы. М. «Наука», 1977.

3.Градштейн И. С. и Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. М., «Наука», 1971.

Таким образом, если требуется вычислить некоторый неопределенный интеграл, то его можно просто поискать в справочнике. Если же нужного интеграла в справочнике нет, то этот интеграл, так или иначе, стараются свести к одному или нескольким табличным интегралам. О методах такого сведения мы поговорим в следующем параграфе.

А сейчас пока лишь отметим следующее важное обстоятельство, связанное с интегрированием функций (с вычислением неопределенных интегралов) и отличающее интегрирование от дифференцирования. Производная любой элементарной функции всегда может быть найдена, и она опять же элементарная функция. А вот неопределенный интеграл не от всякой элементарной функции может быть записан через элементарные функции вида F(X)+C . Иначе говоря, не всякий неопределенный интеграл может быть сведен к табличным. А стало быть, не всякий неопределенный интеграл может быть вычислен в явном виде. Такие, не сводимые к табличным, неопределенные интегралы называются Неберущимися (ибо вычислить неопределенный интеграл – это, на математическом жаргоне, «взять» интеграл). Неберущимися являются многие, даже совсем простые на первый взгляд, неопределенные интегралы. Например, такие:

1. - интеграл Пуассона

2. - интегральный логарифм (1.12)

3. - интегральный косинус.

4. - интегральный синус.

Эти и другие неберущиеся интегралы не могут быть найдены точно. Они могут быть найдены лишь приближенно. В соответствии с равенством (1.3) нахождение неопределенного интеграла сводится к нахождению какой-либо первообразной для подынтегральной функции. Вот эту первообразную для подынтегральной функции можно, используя машинные методы, подобрать приближенно с любой степенью точности. Конкретнее об этом будет сказано в §4.

Упражнения

1. Показать, что на всей числовой оси Ох функция является первообразной для функции .

2. Найти все первообразные для функции

Ответ: .

3. Верно ли равенство:

Ответ: верно.

4.Найти функцию , если и .

Ответ:.

< Предыдущая		Следующая >