4.11. Исследование функций с помощью производных

Теорема 1. Если функция возрастает на некотором интервале оси Ох (с ростом X растет и Y) и дифференцируема на этом интервале, то для любого X из этого интервала (производная имеет знак (+)). А если она убывает на этом интервале (Y убывает с ростом X) и дифференцируема на нем, то для любого X из этого интервала (производная имеет знак (–)).

Доказательство.

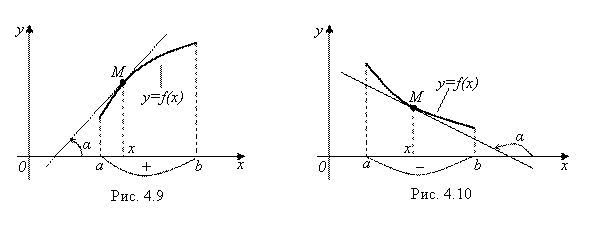
Рассмотрим сначала рис. 4.9. На нем изображен график возрастающей и дифференцируемой на интервале функции . В каждой точке M этого графика касательная составляет с осью Ох острый угол (). Но тангенсы острых углов, как известно, положительны. Значит, согласно геометрического смысла производной (1.11), и производная положительна для любых X из интервала возрастания функции.

А теперь рассмотрим рис. 4.10, на котором изображен график убывающей на интервале функции . Здесь для любой точки М графика функции (а значит, для любого X из интервала ) угол наклона касательной, проведенной к графику функции, тупой (). Но тангенсы таких углов отрицательны. А значит, согласно (1.11), и производная отрицательна.

Следствие теоремы 1. Если на некотором интервале оси Ох в любой его точке X производная функции положительна, то функция возрастает на этом интервале. А если отрицательна – то убывает. Это следствие играет очень важную роль в исследовании функций. Оно позволяет по знаку производной функции определять, растет или убывает функция, и где именно (для каких X) растет, и где (для каких X) убывает.

Пример 1. Рассмотрим функцию . Ее производная . Она положительна при и отрицательна при . Значит, при функция возрастает, а при она убывает. График этой функции (парабола) наглядно подтверждает сказанное.

< Предыдущая		Следующая >