4.08. Производная функции, заданной параметрически

Если функция задана в параметрической форме

, (2.8)

То ее производную находят по формуле:

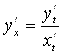. (2.9)

Подтвердим эту формулу. Пусть и – дифференцируемые функции параметра T. Зафиксируем некоторое T, а затем придадим ему приращение . При этом X и Y получат некоторые приращения и , причем при и , и (функции и – дифференцируемые, а значит, и непрерывные). А тогда

.

Пример 13. Функция , заданная параметрически уравнениями

,

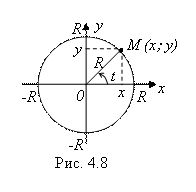
Представляет собой параметрическое уравнение окружности с центром в начале координат и радиусом R (рис. 4.8).

Найдем производную этой функции:

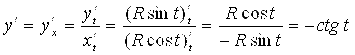
< Предыдущая		Следующая >