3.9. Бесконечно большие функции и их сравнение

Пусть

и , (4.14)

То есть функции и при по абсолютной величине стремятся к бесконечности. Тогда они называются Бесконечно большими при .

Сравнивают бесконечно большие функции по тому же принципу, что и бесконечно малые. А именно:

1) Если

, (4.15)

То функция называется бесконечно большой функцией Низшего порядка роста, чем бесконечно большая функция . А функция – соответственно Высшего порядка роста, чем .

В частности, очевидно, что функции ; ; ; являются бесконечно большими при , причем каждая последующая из них – высшего порядка роста, чем предыдущая. И вообще, можно доказать (см. главу 4, §4), что любая степенная функция () при является бесконечно большой функцией низшего порядка роста, чем любая показательная функция (). То есть

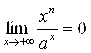(; ) (4.16)

Иначе говоря, Любая показательная функция () при растет быстрее, чем любая степенная функция ().

2) Если

, (4.17)

То бесконечно большие функции и называется Эквивалентными (равносильными), и обозначается это так:

, при (4.18)

3) Если

, (4.19)

Где А – конечное число, и , то функции и называется функциями Одного порядка роста. При этом, очевидно, что

при (4.20)

4) Если и при , то, как и для бесконечно малых функций, получаем равенство, аналогичное (4.13):

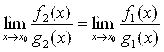(4.21)

Пример 5. Показать, что при :

А) ; б) ; в)

Доказательство. Учтем, что (4.18) равносильно (4.17), и вычислив соответствующие пределы, убедимся, что все они равны 1:

А) ;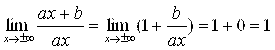

Б) ;

В) .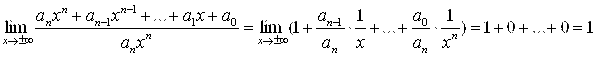

Пример 6.

.

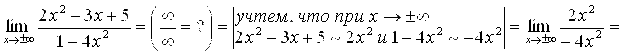
Упражнения

1. Показать, что сумма и произведение любого конечного числа бесконечно малых функций тоже являются бесконечно малыми функциями.

2. Показать, что произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.

3. Доказать, что бесконечно малые при Функции и 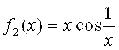несравнимы между собой, то есть что предел их отношения не существует.

4. Показать, что функция при .

5. Показать, что при .

6. Сравнить бесконечно большие функции и при .

Ответ: при .

< Предыдущая		Следующая >