2.14. Частные коэффициенты корреляции

Если переменные X и Y коррелированны не только с величиной Z (ρxz ≠ 0; ρyz ≠ 0), но и между собой (ρxy ≠ 0), то на величине выборочных парных коэффициентов линейной корреляции ρxz И ρyz сказывается не только коррелированность X с Z и Y с Z соответственно, но и коррелированность (взаимозависимость) величин X и Y между собой. Чтобы очистить корреляцию X с Z от влияния Y и корреляцию Y С Z от влияния X, рассматривают так называемую Частную корреляцию между Z и одной из переменных X и Y при исключении влияния (Элиминировании) другой переменной. То есть при условии, что эта другая переменная не меняется. Указанная частная корреляция оценивается с помощью так называемых Выборочных частных коэффициентов линейной корреляции ρxz (Y) (здесь Y =const) и ρyz(X) (здесь X=const):

(5.68)

Частные коэффициенты линейной корреляции (5.68), как и парные коэффициенты ρxz и ρyz , определяемые формулами (5.63), по своим свойствам аналогичны обычному выборочному коэффициенту линейной корреляции ρxy, оценивающему наличие и тесноту линейной корреляционной связи между случайными величинами X И Y. Их возможные значение заключены в пределах [-1;1]. Когда, например, ρxz (Y)=0, то выборка указывает на отсутствие линейной корреляционной зависимости Z От X (при постоянном Y), хотя нелинейная корреляционная и даже функциональная зависимость Z от X остаются возможными. Если же ρxz (Y)= 1 или ρxz (Y)= -1, то выборка указывает на строгую линейную функциональную зависимость Z от X (соответственно возрастающую или убывающую) при постоянном Y. И т. д.

Кстати, и парные ρxz , ρyz , и частные ρxz (Y), ρyz(X) коэффициенты линейной корреляции по своей абсолютной величине не больше, чем множественный коэффициент линейной корреляции R=Rz,Xy.

Множественный коэффициент, равно как и парные, и частные коэффициенты линейной корреляции используются лишь для оценки наличия и степени тесноты линейной корреляционной зависимости Z от X и Y. Степень же тесноты Любой (а не только линейной) корреляционной зависимости Z От X И Y оценивается с помощью Совокупного выборочного корреляционного отношения :

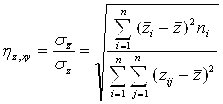(5.69)

Оно показывает, какую долю составляет средний разброс выборочных средних вокруг общей средней по отношению к среднему разбросу всех выборочных значений величины Z вокруг той же общей средней . Формула (5.69) по своему смыслу аналогична формуле (5.22), записанной для случая, когда исследуется парная корреляционная зависимость одной величины от другой (Y от X). Аналогичны и свойства определяемых этими формулами корреляционных отношений. А именно:

А) возможные значения зАключены в пределах [0;1].

Б) если =0, то это значит что все (I=1,2,…N). То есть все выборочные средние величины Z одинаковы для всех выборочных пар (Xi; Yi) значений величин (X;Y). Но это говорит о том, что в выборке величина Z корреляционно (в среднем) не зависит от величин X и Y. Что, в свою очередь, свидетельствует в пользу аналогичной корреляционной независимости Z От X и Y и в генеральной совокупности.

В) если =1, то это значит, что . То есть весь разброс значений Zij Величины Z В выборке сосредоточен в разбросе средних выборочных . Разброс значений Zij вокруг их средних , таким образом, отсутствует, что указывает на некую жесткую функциональную зависимость Z=F(X;Y) величины Z от X и Y.

Если в формуле (5.69) заменить реальные выборочные средние на сглаживающие средние , вычисленные по подобранному сглаживающему уравнению регрессии (5.54), и возвести полученное выражение в квадрат, то получим так называемый Совокупный выборочный коэффициент детерминации:

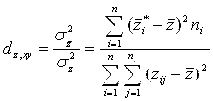(5.70)

Совокупный выборочный коэффициент детерминации (5.70) показывает, какую долю вариации (изменения) исследуемой величины Z объясняет в выборке подобранное сглаживающее уравнение регрессии (5.54). Чем этот коэффициент больше, тем лучшим считается подобранное выборочное уравнение регрессии (5.54), сглаживающее выборочные данные (5.52). Формула (5.70) и её смысл аналогичен формуле (5.23), полученной при исследовании парной корреляционной зависимости одной величины от другой (Y от X).

Кстати, имеют место и аналоги равенств (5.24) и (5.25). В частности:

5.71)

Если сглаживающее уравнение регрессии (5.54) строится в линейной форме (5.56), то совокупный выборочный коэффициент детерминации можно найти не только по общей формуле (5.70), но и по частной формуле:

(5.72)

Являющейся аналогом формулы (5.25).

< Предыдущая		Следующая >