2.15. Адекватность выборочного сглаживающего уравнения регрессии
Построив с помощью метода наименьших квадратов некое сглаживающее выборочное уравнение регрессии (5.54) – например, в линейной форме (5.56) или в какой-то нелинейной форме, мы затем должны проверить его на адекватность выборочным данным (5.52). То есть сделать то, что делалось выше для случая парной корреляции (формулы (5.31 - 5.36)). Для этого:
А) Находим суммы QПовт и QАдекв:
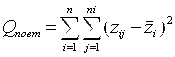 ;
;  (5.73)
(5.73)
Б) Находим дисперсии повторности и адекватности
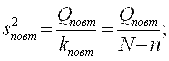
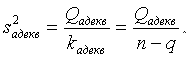 (5.74)
(5.74)
Где Q- число оцениваемых по выборочным данным коэффициентов подобранного сглаживающего уравнения регрессии (5.54) (в случае (5.56) Q = 3);
В) Находим
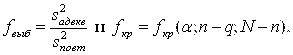 (5.75)
(5.75)
Где ![]() - табличное критическое значение критерия Фишера – Снедекора. И если окажется, что
- табличное критическое значение критерия Фишера – Снедекора. И если окажется, что ![]() , то подобранное уравнение регрессии (5.54) признаем адекватным выборочным данным (при заданном уравнение значимости
, то подобранное уравнение регрессии (5.54) признаем адекватным выборочным данным (при заданном уравнение значимости ![]() ). А если окажется, что
). А если окажется, что ![]() , то это уравнение считаем неадекватным, а следовательно, непригодным для оценки истинного (генерального) уравнения регрессии.
, то это уравнение считаем неадекватным, а следовательно, непригодным для оценки истинного (генерального) уравнения регрессии.
Наряду с проверкой адекватности выборочного сглаживающего уравнения регрессии В целом имеется возможность проверить и значимость Каждого его коэффициента в отдельности. Это значит имеется возможность установить, достаточно ли велико по модулю подсчитанное значение интересующего нас коэффициента для статистически обоснованного вывода о том, что он отличен от нуля. То есть значим ли он (нужно его учитывать) или он незначим и учитывать его не нужно. И если окажется, что коэффициент незначим, то его можно положить равным нулю. Это приведёт к упрощению подобранного уравнения регрессии без существенного ущерба для его качества.
Но на этом мы не останавливаемся. Отметим лишь, что такое исследование проводится автоматически, если выборочное сглаживающее уравнение регрессии строится с помощью стандартной программы корреляционно-регрессионного анализа на ЭВМ. В уравнении регрессии, выдаваемом машиной, фигурируют лишь значимые коэффициенты, а заодно и указывается, адекватно ли всё уравнение в целом.
Упражнения.
1. Пусть при исследовании корреляционной зависимости X от Y получено 2N точек корреляционного поля, расположенных симметрично относительно некоторой прямой Y = Kx + B и удаленных от неё в направлении оси Oy на ±δ (см. рис. 3.14).  Требуется:
Требуется:
1) Найти выборочное сглаживающее уравнение регрессии ![]() ;
;
2) Найти выборочный коэффициент линейной корреляции ![]()
3) Найти выборочное корреляционное отношение ![]()
4) Найти выборочный коэффициент детерминации ![]()
5) Исследовать вопрос об адекватности выборочным данным найденного уравнения регрессии.
Ответ: 1) ![]() - точное сглаживающее выборочное уравнение регрессии;
- точное сглаживающее выборочное уравнение регрессии;
2)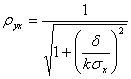 ; 3)
; 3)![]() ; 4)
; 4)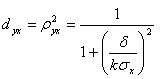 ;
;
5) Выборочное уравнение регрессии ![]() адекватно выборочным данным при любом уровне значимости
адекватно выборочным данным при любом уровне значимости ![]() .
.
2. При исследовании корреляционной зависимости урожайности некоторой культуры Y (Ц/га) от глубины орошения X (См) получена следующая корреляционная таблица:
|
|
0 |
10 |
20 |
30 |
40 |
50 |
|
|
10 |
4 |
- |
- |
- |
- |
2 |
6 |
|
12 |
1 |
2 |
1 |
2 |
2 |
2 |
10 |
|
14 |
- |
3 |
4 |
2 |
3 |
2 |
14 |
|
16 |
- |
2 |
4 |
3 |
1 |
- |
10 |
|
|
5 |
7 |
9 |
7 |
6 |
6 |
N=40 |
Построить корреляционное поле, соответствующее данной корреляционной таблице. С его помощью из уравнений (5.5) - (5.7) выбрать наиболее подходящую форму для построения выборочного сглаживающего уравнения регрессии ![]() И построить это уравнение. Найти выборочное корреляционное отношение
И построить это уравнение. Найти выборочное корреляционное отношение ![]() И выборочный коэффициент детерминации
И выборочный коэффициент детерминации ![]() . При уровне значимости
. При уровне значимости ![]() проверить гипотезу об адекватности полученного выборочного уравнения регрессии.
проверить гипотезу об адекватности полученного выборочного уравнения регрессии.
Ответ. По конфигурации корреляционного поля, а также по смыслу рассматриваемых величин X И Y наиболее подходящей формой для выборочного уравнения регрессии является параболическая форма (5.7). Коэффициенты (А0; а1; а2) уравнения (5.7) находятся из решения нормальной системы (5.30). Для формирования матрицы этой системы рекомендуется по данным заданной корреляционной таблицы составить следующую вспомогательную таблицу:
|
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
10,4 |
0 |
0 |
0 |
0 |
52 |
0 |
0 |
|
10 |
7 |
14 |
70 |
700 |
7000 |
70000 |
98 |
980 |
9800 |
|
20 |
9 |
44/3 |
180 |
3600 |
72000 |
1440000 |
132 |
2640 |
52800 |
|
30 |
7 |
100/7 |
210 |
6300 |
189000 |
5670000 |
100 |
3000 |
90000 |
|
40 |
6 |
41/3 |
240 |
9600 |
384000 |
15360000 |
82 |
3280 |
131200 |
|
50 |
6 |
12 |
300 |
15000 |
750000 |
37500000 |
72 |
3600 |
180000 |
|
|
40 |
- |
1000 |
35200 |
1402000 |
60040000 |
536 |
13500 |
463800 |
В итоге (убедитесь в этом) получаем следующее выборочное уравнение регрессии:
![]()
![]()
При этом
![]()
![]()
Найденное выборочное уравнение регрессии адекватно выборочным данным, причем не только для уровня значимости ![]() , но и вообще для любого уровня значимости. Действительно, используя формулы (5.33) - (5.36) и данные предыдущих таблиц получаем:
, но и вообще для любого уровня значимости. Действительно, используя формулы (5.33) - (5.36) и данные предыдущих таблиц получаем:


![]()
![]()
![]()
![]()
Но табличное значение критерия Фишера-Снедекора ![]() для любых значений
для любых значений ![]() . Поэтому
. Поэтому ![]() для любых значений
для любых значений ![]() . А значит, выборочное уравнение регрессии адекватно выборочным данным при любом
. А значит, выборочное уравнение регрессии адекватно выборочным данным при любом ![]() .
.
3. Выборочным путем исследовалась корреляционная зависимость некоторой случайной величины Z От двух других случайных величин X и Y. Данные выборки (корреляционная таблица) представлены в первых четырех столбцах таблицы, приводимой ниже:
|
I |
Xi |
Yi |
Zi |
Xi yi |
Xizi |
Yizi |
|
|
|
|
1 |
25,5 |
17,3 |
85,5 |
441,15 |
2180,25 |
1479,15 |
650,25 |
229,29 |
7310 |
|
2 |
34,1 |
19,8 |
81,7 |
665,18 |
2785,97 |
1617,66 |
1162,81 |
392,04 |
6675 |
|
3 |
37,3 |
30,1 |
71,7 |
1122,73 |
2674,41 |
2158,17 |
1391,29 |
906,01 |
5141 |
|
4 |
44,7 |
31,9 |
62,7 |
1425,93 |
2802,69 |
2000,13 |
1998,09 |
1017,61 |
3931 |
|
5 |
44,6 |
38,3 |
66,4 |
1708,18 |
2961,44 |
2543,12 |
1989,16 |
1466,89 |
4409 |
|
6 |
41,0 |
26,5 |
70,6 |
1086,50 |
2894,60 |
1870,90 |
1681,00 |
702,25 |
4984 |
|
7 |
49,5 |
36,2 |
65,0 |
1791,90 |
3217,50 |
2353,00 |
2450,25 |
1310,44 |
4225 |
|
8 |
45,1 |
21,0 |
72,8 |
947,10 |
3283,28 |
1528,80 |
2034,01 |
441,00 |
5300 |
|
9 |
56,5 |
29,5 |
67,6 |
1666,75 |
3819,40 |
1994,20 |
3192,25 |
870,25 |
4570 |
|
10 |
35,4 |
29,4 |
90,0 |
881,46 |
3186,00 |
2241,00 |
1253,16 |
620,01 |
8100 |
|
11 |
54,9 |
25,0 |
60,2 |
1372,50 |
3304,98 |
1505,00 |
3014,01 |
625,00 |
3624 |
|
12 |
32,8 |
28,0 |
74,8 |
918,40 |
2453,44 |
2094,40 |
1075,84 |
784,00 |
5595 |
|
13 |
55,5 |
33,9 |
63,4 |
1881,45 |
3518,70 |
2149,26 |
3080,25 |
1149,21 |
4020 |
|
14 |
41,5 |
16,1 |
74,2 |
668,15 |
3079,30 |
1194,62 |
1722,25 |
259,21 |
5506 |
|
15 |
41,5 |
21,0 |
71,6 |
871,50 |
2971,40 |
1503,60 |
1722,25 |
441,00 |
5127 |
|
16 |
52,7 |
28,7 |
60,0 |
1512,49 |
3162,00 |
1722,00 |
2777,49 |
823,69 |
3600 |
|
17 |
37,9 |
20,3 |
81,1 |
769,37 |
3073,69 |
1646,33 |
1436,41 |
412,09 |
6577 |
|
18 |
43,9 |
19,9 |
71,5 |
873,61 |
3138,85 |
1422,85 |
1927,21 |
396,01 |
5112 |
|
19 |
35,0 |
22,6 |
77,2 |
791,00 |
2702,00 |
1744,72 |
1225,00 |
510,76 |
5960 |
|
20 |
27,8 |
20,1 |
91,2 |
558,78 |
2535,36 |
1833,12 |
772,84 |
404,01 |
8317 |
|
|
837,2 |
511,1 |
1459,2 |
21964,13 |
59745,26 |
36602,03 |
36555,62 |
13830,77 |
108083 |
Требуется:
1) Построить выборочное сглаживающее уравнение регрессии ![]() в линейной форме (5.56).
в линейной форме (5.56).
2) Найти совокупный выборочный коэффициент линейной корреляции R и частные выборочные коэффициенты линейной корреляции ![]() и
и ![]() .
.
3) Найти выборочный коэффициент детерминации ![]() .
.
4) Оценить адекватность выборочным данным построенного уравнения регрессии.
Ответ:
1) Искомое выборочное уравнение регрессии имеет вид
![]()
Его можно получить, или составив и решив для коэффициентов (A;B;C) уравнения (5.56) нормальную систему (5.59) (используя для этого результаты приведенной выше таблицы), или воспользовавшись формулами (5.60) - (5.65).
2) R=0,877; ![]() = 0,792;
= 0,792; ![]() =0,374; 3)
=0,374; 3)![]() = R2 = 0.769;
= R2 = 0.769;
4) Адекватность полученного выборочного уравнения регрессии проверить невозможно, так как корреляционная таблица не содержит результатов повторных опытов для одних и тех же (Xi ; YI), а следовательно, невозможно найти дисперсию повторности ![]() .
.
| < Предыдущая | Следующая > |
|---|