2.13. Множественная корреляция
Перейдем теперь к случаю, когда выборочным путем изучается корреляционная зависимость (зависимость в среднем) одной величины от нескольких других (множественная корреляция). Ограничимся рассмотрением случая, когда изучается корреляционная зависимость некоторой величины Z От двух величин X и Y.
Будем считать, что при изучении этой зависимости проведено N Различных опытов, в которых измерялись значения всех трех величин и в которых пары (Xi; Yi) (I=1,2… N) значений величин X И Y варьировались следующим образом:
|
I |
1 |
2 |
3 |
… |
N |
(5.50) |
|
Xi |
X1 |
X2 |
X3 |
… |
Xn | |
|
Yi |
Y1 |
Y2 |
Y3 |
… |
Yn |
Далее, будем считать, что каждый из этих опытов (при фиксированных (Xi; Yi)) повторен некоторое (не обязательно одинаковое) число раз Ni. Повторные опыты при одних и тех же значениях (Xi; Yi) дают, вообще говоря, различные значения Zij (J=1,2,…Ni) величины Z. Пусть
 (I=1,2…N) (5.51)
(I=1,2…N) (5.51)
- среднее их значение для каждого I-го опыта. В итоге совокупность всех опытных данных (корреляционная таблица) примет вид:
|
I (номер опыта) |
1 |
2 |
3 |
…. |
N |
(5.52) |
|
Ni (повторность Опыта) |
N1 |
N2 |
N3 |
…. |
Nn | |
|
Xi |
X1 |
X2 |
X3 |
…. |
Xn | |
|
Yi |
Y1 |
Y2 |
Y3 |
…. |
Yn | |
|
|
|
|
|
…. |
|
Заметим, что общее количество N всех проведенных опытов найдется, очевидно, по формуле:
 (5.53)
(5.53)
Основные задачи корреляционно – регрессионного анализа при множественной корреляции те же, что и при парной.
В частности, Первой основной задачей по исследованию корреляционной зависимости Z От X и Y является построение выборочного уравнения регрессии
![]() , (5.54)
, (5.54)
Наилучшим образом выравнивающего (сглаживающего) выборочные данные, а следовательно, являющегося наилучшим приближением Истинного (генерального) Уравнения регрессии
![]()
![]() (5.55)
(5.55)
Заметим, что геометрически этому генеральному уравнению регрессии соответствует уже не линия регрессии на плоскости Хоу, а Поверхность регрессии в пространстве (X; Y; Z)
Второй основной задачей является оценка тесноты корреляционной зависимости Z от X и Y.
Ограничимся рассмотрением случая, когда наилучшее сглаживающееся уравнение регрессии (5.54) строится в линейной форме
![]() (5.56)
(5.56)
То есть когда уравнение поверхности в пространстве (5.55) приближается (приближенно заменяется) уравнением плоскости в пространстве (5.56). Параметры (А;B;с) этого уравнения находятся, как обычно, методом наименьших квадратов:
 (5.57)
(5.57)
Реализация необходимых условий минимума функции Q
 (5.58)
(5.58)
Приводит к следующей системе трех линейных уравнений с тремя неизвестными (А;B;с) (к так называемой Нормальной системе):
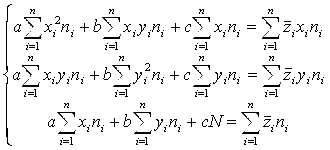 (5.59)
(5.59)
Решая эту нормальную систему, находим (А;B;с), а вместе с ними находим и наилучшее линейное уравнение (5.56), сглаживающее выборочные данные корреляционной таблицы (5.52). В своем окончательном виде оно таково:
![]() (5.60)
(5.60)
Здесь
 (5.61)
(5.61)
- выборочные средние величин X, Y и Z соответственно, а коэффициенты а и B находится по формулам:
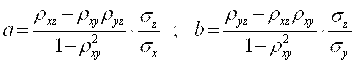 (5.62)
(5.62)
При этом
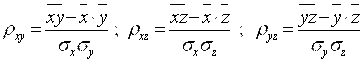 (5.63)
(5.63)
- выборочные значения парных коэффициентов линейной корреляции между соответствующими парами величин X, Y, Z, а
![]() (5.64)
(5.64)
- выборочные значения среднеквадратических отклонений величин X, Y и Z Соответственно. При подсчете выражений (5.63) и (5.64) используются аналогичные (5.13) формулы:
 (5.65)
(5.65)
Вторая основная задача – установление тесноты линейной корреляционной зависимости Z От X и Y – решается с помощью так называемого Совокупного коэффициента линейной корреляции R(Z, XY) (или просто R), выборочное значение которого находится по формуле:

(5.66)
Доказано, что:
1. Совокупный коэффициент линейной корреляции имеет возможные значения в промежутке [0;1].
2. Если R=0, то Z не может быть связана с X и Y линейной корреляционной зависимостью. Однако при этом возможна нелинейная корреляционная и даже функциональная зависимость Z от X и Y.
3. Если R=1, то Z связана с X и Y линейной функциональной зависимостью вида
![]() (5.67)
(5.67)
Для выборочных данных (Xi; Yi; Zij) последний случай означает, что все повторные (для разных J) значения Zij Совпадают и равны одному и тому же значению ![]() , а все пространственные точки (Xi; Yi;
, а все пространственные точки (Xi; Yi; ![]() ) располагаются на одной и той же плоскости – а именно, на плоскости (5.56) (или, что одно и то же, на плоскости (5.60)).
) располагаются на одной и той же плоскости – а именно, на плоскости (5.56) (или, что одно и то же, на плоскости (5.60)).
4. Если R отличен от своих крайних значений (0 и 1), то при приближении R к единице теснота линейной корреляционной зависимости Z от X и Y увеличивается. Это значит, что экспериментальные пространственные точки (Xi; Yi; Zij) все теснее примыкают к плоскости (5.60).
| < Предыдущая | Следующая > |
|---|