2.12. Парная корреляция
Начнем с наиболее простого случая. Пусть с помощью выборки объемом N изучались объекты генеральной совокупности, каждый из которых характеризуется двумя (парой) Количественных признаков X И Y. Подчеркиваем: Количественных, ибо если эти признаки качественные, то исследование их взаимозависимости – это задача дисперсионного анализа. Например, если объектами генеральной совокупности являются изделия некоторого массового производства, то их количественными признаками X И Y могут быть, например, каких-то два их контролируемых размера; или размер и вес; или затраты на производство и выручка от продажи, и т. д. Выборочные данные оформляют в виде таблицы (5.1):
|
Xi Yj |
X1 |
X2 |
… |
Xn |
|
(5.1) |
|
Y1 |
N11 |
N21 |
… |
Nn1 |
M1 | |
|
Y2 |
N12 |
N22 |
… |
Nn2 |
M2 | |
|
… |
… |
… |
… |
… |
… | |
|
Ym |
N1m |
N2m |
… |
Nnm |
Mm | |
|
|
N1 |
N2 |
… |
Nn |
|
Эта таблица называется Корреляционной. Из нее видно, что признак Х у объектов выборки принимал значения Xi = (X1 ; X2 ; … Xn ), а признак Y – значения Yj = (Y1 ; Y2 ; … Ym ), причем пара значений (X1; Y1) встретилась у N11 Объектов, пара (X2; Y1) – у N21 Объектов, и т. д. Числа Ni = (N1 ; N2 ; … Nn ) определяют общее количество объектов выборки со значениями признака Х, равными (X1 ; X2 ; … Xn ) Соответственно, а числа (M1; M2; … Mm ) – общее количество объектов со значениями (Y1 ; Y2 ; … ; Ym ) признака Y соответственно. При этом ясно, что
|
|
Корреляционная таблица (5.1) фактически является статистическим распределением выборки при исследовании двумерного (двухпараметрического) признака Z=(X, Y) объектов генеральной совокупности.
Данные корреляционной таблицы для наглядности удобно изобразить и в виде так называемого Корреляционного поля. Корреляционное поле – это нанесенное на плоскость Xoy множество всех N экспериментальных точек с координатами (Xi; Yj) с учетом их кратности Nij. Это значит, что при построении корреляционного поля нужно показать, что в точке (Xi; Yj) плоскости Xoy содержится не одна, а Nij точек. Чтобы это было видно на корреляционном поле, нужно эти точки немного отделить друг от друга. Они тогда образуют видимую компактную кучку из Nij точек, окружающих точку (Xi; Yj )(рис.3.11).

Рис. 3.11
Как мы знаем из части I (§6, глава 2), корреляционную зависимость (зависимость в среднем) величины Y от величины X характеризует так называемое Уравнение регрессии ![]() величины Y на величину X. А график этого уравнения называется Линией регрессии Y на Х. Примерный (оценочный) вид этой линии мы получим, если по данным корреляционной таблицы (5.1) для каждого выборочного значения X=Xi Найдем среднее значение
величины Y на величину X. А график этого уравнения называется Линией регрессии Y на Х. Примерный (оценочный) вид этой линии мы получим, если по данным корреляционной таблицы (5.1) для каждого выборочного значения X=Xi Найдем среднее значение ![]() величины Y
величины Y
|
|
И затем нанесем на корреляционное поле ломаную, соединяющую точки с координатами ![]()
![]() – рис. 3.11. Эта ломаная называется Выборочной линией регрессии Y на X. Построив эту линию, визуально можем оценить и наличие, и тесноту корреляционной зависимости Y От Х: чем меньше разброс точек корреляционного поля вокруг выборочной линии регрессии Y на Х, тем эта зависимость теснее.
– рис. 3.11. Эта ломаная называется Выборочной линией регрессии Y на X. Построив эту линию, визуально можем оценить и наличие, и тесноту корреляционной зависимости Y От Х: чем меньше разброс точек корреляционного поля вокруг выборочной линии регрессии Y на Х, тем эта зависимость теснее.
Задачи корреляционно-регрессионного анализа в математической статистике аналогичны тем, что были поставлены в теории вероятностей (§6, глава 2). Этих задач две.
Задача 1. Дать оценку истинного (генерального) уравнения регрессии ![]() величины Y на величину Х. А следовательно, дать и оценку истинной (генеральной) линии регрессии Y на Х. Мы говорим лишь об оценке, ибо найти точно по выборочным данным и генеральное уравнение регрессии, и генеральную линию регрессии, очевидно, невозможно.
величины Y на величину Х. А следовательно, дать и оценку истинной (генеральной) линии регрессии Y на Х. Мы говорим лишь об оценке, ибо найти точно по выборочным данным и генеральное уравнение регрессии, и генеральную линию регрессии, очевидно, невозможно.
Задача 2. Оценить степень тесноты корреляционной зависимости Y от Х.
Начнем с рассмотрения первой из этих задач. Идея ее решения состоит в подборе возможно простого уравнения
|
|
График которого тем не менее будет достаточно близким к выборочной линии (ломаной) регрессии. То есть будет достаточно хорошим приближением этой ломаной, сглаживающим эту ломаную. Такое уравнение называется Выравнивающим (или Сглаживающим) выборочным уравнением регрессии. Именно оно и принимается за оценку истинного (генерального) уравнения регрессии ![]() , то есть за решение первой задачи корреляционно-регрессионного анализа.
, то есть за решение первой задачи корреляционно-регрессионного анализа.
Отметим, однако, что два указанных выше требования: а) простота сглаживающего уравнения регрессии (5.4), а значит, и простота сглаживающей линии регрессии, и б) близость сглаживающей линии регрессии к реальной ломаной регрессии, вообще говоря, противоречивы, ибо повысить указанную близость можно лишь за счет усложнения сглаживающего уравнения. Поэтому на практике стараются добиться некоей золотой середины: и чтобы сглаживающее уравнение регрессии (5.4) было не слишком сложным, и чтобы соответствующая ему сглаживающая линия регрессии тем не менее в целом была достаточно близкой к выборочной ломаной регрессии. Как из многих возможных вариантов выбрать лучший (найти эту золотую середину) – об этом будет сказано ниже.
В качестве наиболее простых форм сглаживающего уравнения (5.4) чаще всего принимаются следующие его формы:
1) Уравнение прямой
|
|
2) Уравнение гиперболы
|
|
3) Уравнение параболы
|
|
Напомним, что эти линии в принципе имеют следующий вид:
|
|
  |
|
Линейная зависимость (5.5) ![]() наиболее проста по форме, ее параметры K И B Легко интерпретируются. В частности, коэффициент K указывает, на сколько в среднем увеличится (при K>0) или уменьшится (при K<0) величина Y, если значение Х величины Х увеличится на единицу. А параметр B указывает среднее значение величины Y при Х = 0. Благодаря этим преимуществам, а также благодаря простоте вычисления параметров K И B уравнение (5.5) используется в качестве приближенного (сглаживающего) уравнения регрессии даже в тех случаях, когда более логичным представляется использование уравнение кривой.
наиболее проста по форме, ее параметры K И B Легко интерпретируются. В частности, коэффициент K указывает, на сколько в среднем увеличится (при K>0) или уменьшится (при K<0) величина Y, если значение Х величины Х увеличится на единицу. А параметр B указывает среднее значение величины Y при Х = 0. Благодаря этим преимуществам, а также благодаря простоте вычисления параметров K И B уравнение (5.5) используется в качестве приближенного (сглаживающего) уравнения регрессии даже в тех случаях, когда более логичным представляется использование уравнение кривой.
Гиперболы (5.6) – это либо монотонно возрастающая, либо монотонно убывающая кривая. Однако, в отличие от прямой, рост или убывание гиперболы имеет тенденцию к затуханию, практически сходя на нет при больших значениях Х величины Х. Параметр B при этом представляет собой предельное значение ![]() при X ® ¥. Убывающей гиперболой, например, хорошо выражается зависимость себестоимости продукции растениеводства от урожайности, а возрастающей – зависимость продуктивности животных от расхода кормов.
при X ® ¥. Убывающей гиперболой, например, хорошо выражается зависимость себестоимости продукции растениеводства от урожайности, а возрастающей – зависимость продуктивности животных от расхода кормов.
Парабола (5.7) имеет вершину или впадину и применяется для приближенной описания зависимостей, в которых с изменением Х убывание ![]() может меняться на возрастание, и наоборот. Примером параболической зависимости является, например, зависимость средней урожайности от дозы удобрений, когда начальные дозы удобрений приводят к значительному увеличению урожая, последующие – к постепенно уменьшающимся прибавкам, а чрезмерные – к снижению урожая и даже к его гибели. Иногда график параболы используется только частично (только восходящая или только нисходящая ветвь). Параметры параболы, за исключением А0, интерпретировать сложно. Ну, а параметр А0 является, очевидно, оценкой среднего значения величины Y при Х = 0.
может меняться на возрастание, и наоборот. Примером параболической зависимости является, например, зависимость средней урожайности от дозы удобрений, когда начальные дозы удобрений приводят к значительному увеличению урожая, последующие – к постепенно уменьшающимся прибавкам, а чрезмерные – к снижению урожая и даже к его гибели. Иногда график параболы используется только частично (только восходящая или только нисходящая ветвь). Параметры параболы, за исключением А0, интерпретировать сложно. Ну, а параметр А0 является, очевидно, оценкой среднего значения величины Y при Х = 0.
Подходящую форму сглаживающего уравнения регрессии ![]() выбирают, исходя из общих теоретических соображений или, что чаще, по виду корреляционного поля (рис. 3.11). При этом, как уже говорилось выше, наиболее часто уравнение регрессии выбирается в одной из форм (5.5) – (5.7). А для нахождения параметров выбранного уравнения используется универсальный стандартный метод, называемый Методом наименьших квадратов.
выбирают, исходя из общих теоретических соображений или, что чаще, по виду корреляционного поля (рис. 3.11). При этом, как уже говорилось выше, наиболее часто уравнение регрессии выбирается в одной из форм (5.5) – (5.7). А для нахождения параметров выбранного уравнения используется универсальный стандартный метод, называемый Методом наименьших квадратов.
Суть этого метода в следующем. Из корреляционной таблицы (5.1) для каждого Х = хI По формуле (5.3) находим выборочное среднее значение ![]() величины Y. Далее, для выбранной формы уравнения регрессии записываем сглаживающие средние
величины Y. Далее, для выбранной формы уравнения регрессии записываем сглаживающие средние ![]() . В итоге получаем следующую таблицу соответствий экспериментальных
. В итоге получаем следующую таблицу соответствий экспериментальных ![]() и сглаживающих
и сглаживающих ![]() средних значений величины Х, принимающей значения ХI с частотами Ni (I = 1, 2, … N):
средних значений величины Х, принимающей значения ХI с частотами Ni (I = 1, 2, … N):
|
ХI |
X1 |
X2 |
… |
Xn |
(5.8) |
|
Ni |
N1 |
N2 |
… |
Nn | |
|
|
|
|
… |
| |
|
|
|
|
… |
|
Параметры выбранного сглаживающего уравнения регрессии ![]() считаются наилучшими, если они обеспечивают минимально возможные отклонения выборочных средних
считаются наилучшими, если они обеспечивают минимально возможные отклонения выборочных средних ![]() от подсчитанных по уравнению регрессии сглаживающих средних
от подсчитанных по уравнению регрессии сглаживающих средних ![]() . В методе наименьших квадратов за меру отклонений
. В методе наименьших квадратов за меру отклонений ![]() от
от ![]() принимается сумма квадратов их разностей. При этом должно быть учтено, что в образовании каждого
принимается сумма квадратов их разностей. При этом должно быть учтено, что в образовании каждого ![]() участвуют Ni точек корреляционного поля. То есть в средней
участвуют Ni точек корреляционного поля. То есть в средней ![]() как бы сливаются Ni значений величины Y. C Учетом сказанного указанная сумма принимает вид:
как бы сливаются Ni значений величины Y. C Учетом сказанного указанная сумма принимает вид:
|
|
В эту сумму входят параметры выбранной функции ![]() . И эти параметры подбираются таким образом, чтобы сумма Q была минимально возможной. А это – стандартная задача математического анализа об исследовании функции нескольких переменных на экстремум (минимум или максимум), где Q – функция, а ее переменные – параметры функции
. И эти параметры подбираются таким образом, чтобы сумма Q была минимально возможной. А это – стандартная задача математического анализа об исследовании функции нескольких переменных на экстремум (минимум или максимум), где Q – функция, а ее переменные – параметры функции ![]() . Решая эту задачу, находим наилучшие параметры функции
. Решая эту задачу, находим наилучшие параметры функции![]() , а вместе с ними получаем и искомое наилучшее (для выбранной формы) сглаживающее уравнение регрессии (5.4), являющееся оценкой истинного (генерального) уравнения регрессии
, а вместе с ними получаем и искомое наилучшее (для выбранной формы) сглаживающее уравнение регрессии (5.4), являющееся оценкой истинного (генерального) уравнения регрессии ![]() .
.
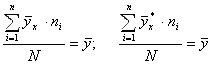
Заметим что и реальные выборочные средние ![]() , и сглаживающие средние
, и сглаживающие средние![]() имеют одно и тоже среднее значение – общую выборочную среднюю
имеют одно и тоже среднее значение – общую выборочную среднюю ![]() величины Y. То есть
величины Y. То есть
|
|
Первое из этих равенств следует из выражения (5.3):

А второе равенство получим, рассудив следующим образом. Так как сглаживающая кривая ![]() получена методом наименьших квадратов в процессе минимизации суммы (5.9), то она наилучшим способом вписывается в выборочную линию регрессии, то есть имеет от нее в целом минимальное отклонение. Поэтому если эту сглаживающую линию поднять или опустить, то есть если заменить на линию
получена методом наименьших квадратов в процессе минимизации суммы (5.9), то она наилучшим способом вписывается в выборочную линию регрессии, то есть имеет от нее в целом минимальное отклонение. Поэтому если эту сглаживающую линию поднять или опустить, то есть если заменить на линию ![]() , где С – некоторая константа, то взамен функции (5.9) получим функцию
, где С – некоторая константа, то взамен функции (5.9) получим функцию
![]()
Значения которой при всех С больше величины (5.9). А свое наименьшее значение (экстремум) функция Q(C) должна иметь при С = 0. Но это значит, что
![]() При
При ![]()
Отсюда следует:

То есть и второе равенство (5.10) доказано.
Равенства (5.10) можно использовать для контроля правильности подсчета и реальных выборочных средних ![]() , и сглаживающих выборочных средних
, и сглаживающих выборочных средних ![]()
Рассмотрим, в частности, приложение метода наименьших квадратов к случаю, когда теоретические соображения или конфигурация корреляционного поля позволяют в качестве сглаживающего уравнения регрессии ![]() использовать уравнение прямой (5.5). Сформируем для этого случая сумму Q:
использовать уравнение прямой (5.5). Сформируем для этого случая сумму Q:
![]()
Вспоминая, что необходимым условием минимума (или максимума) функции нескольких переменных является равенство нулю всех ее частных производных первого порядка, получим следующую систему уравнений (так называемую Нормальную систему) для нахождения параметров K и B Функции (5.5):
|
|
Сократив на (-2) и разделив затем обе части каждого уравнения на N, получим:
|
|
Учтем, что
|
|
Тогда система (5.12) примет вид:
|
|
Решая ее, находим K И B:
|
|
Подставляя найденные значения K И B в уравнение (5.5), получим искомое сглаживающее линейное уравнение регрессии Y На X:
|
|
Отметим, что по своей форме оно точно такое же, как и уравнение (6.22) (часть I, глава 2, §6), полученное нами ранее в теории вероятностей. Совпадают эти уравнения не только по форме, но и по существу.
Действительно, в уравнении (6.22), согласно (6.23), (6.7) и (6.5) главы 2 фигурируют
|
|
Сравнивая эти выражения ![]() с теми выражениями (5.13) и (5.15), что используются в только что полученном уравнении (5.16), видим, что разница между ними состоит лишь в том, что выражения (5.17) дают истинные (генеральные) значения параметров
с теми выражениями (5.13) и (5.15), что используются в только что полученном уравнении (5.16), видим, что разница между ними состоит лишь в том, что выражения (5.17) дают истинные (генеральные) значения параметров ![]() , а выражения (5.13) и (5.15) дают выборочные значения этих же параметров.
, а выражения (5.13) и (5.15) дают выборочные значения этих же параметров.
Кстати, выборочный коэффициент линейной корреляции RXy, являющийся выборочным значением истинного (генерального) коэффициента линейной корреляции R(X, Y) случайных величин X И Y, находится по формуле:
|
|
Или, что то же самое, по формуле, связывающей его с параметром K уравнения (5.16):
|
|
При этом
|
|
– выборочные значения среднеквадратических отклонений S(Х) и S(Y) величин X И Y соответственно, а
|
|
– выборочное значение корреляционного момента (ковариации) M(X,Y) величин X И Y.
Значение RXy выборочного коэффициента линейной корреляции используется, в соответствии с §6 (часть I, глава 2), для оценки степени тесноты и линейности корреляционной связи между случайными величинами X И Y. Степень же тесноты Любой (а не только линейной) корреляционной зависимости Y от X определяет, как мы знаем (§ 6, глава 2, часть I) Корреляционное отношение η(Y, X), чье выборочное значение ηYx, с учетом формулы (6.40) главы 2, находится по формуле:
|
|
Оно показывает долю, которую составляет ![]() по отношение к
по отношение к ![]() . То есть показывает, какую часть составляет средний разброс выборочных средних
. То есть показывает, какую часть составляет средний разброс выборочных средних ![]() вокруг общей средней
вокруг общей средней ![]() величины Y в выборке по отношению к среднему разбросу значений Yj величины Y в выборке вокруг той же общей средней
величины Y в выборке по отношению к среднему разбросу значений Yj величины Y в выборке вокруг той же общей средней ![]() .
.
Минимально возможное значение (HYx)Min = 0 указывает на то, что ![]() . То есть что разброс выборочных средних
. То есть что разброс выборочных средних ![]() вокруг общей средней
вокруг общей средней ![]() отсутствует. А это значит, что
отсутствует. А это значит, что ![]() для всех Xi (I = 1, 2, …, N). Выборочная ломаная регрессии (рис. 3.11) становится в этом случае горизонтальной прямой. Выборочные средние
для всех Xi (I = 1, 2, …, N). Выборочная ломаная регрессии (рис. 3.11) становится в этом случае горизонтальной прямой. Выборочные средние ![]() не меняются с изменением X , а значит, они от Х не зависят. Тогда выборка свидетельствует о том, что, скорее всего, величина Y корреляционно (в среднем) не зависит от величины Х. Мы говорим «скорее всего», потому что никаких окончательных выводов относительно генеральной совокупности исследование выборки дать не может - другая выборка может привести и к другим выводам.
не меняются с изменением X , а значит, они от Х не зависят. Тогда выборка свидетельствует о том, что, скорее всего, величина Y корреляционно (в среднем) не зависит от величины Х. Мы говорим «скорее всего», потому что никаких окончательных выводов относительно генеральной совокупности исследование выборки дать не может - другая выборка может привести и к другим выводам.
Максимально же возможное значение (HYx)Max = 1 указывает на отсутствие разброса значений ![]() величины Y относительно их средних значений
величины Y относительно их средних значений ![]() для каждого ХI (I = 1, 2, …, N). Это означает отсутствие разброса точек корреляционного поля вокруг выборочной линии регрессии (рис. 3.11). То есть в этом случае каждому Xi соответствует лишь одно значение
для каждого ХI (I = 1, 2, …, N). Это означает отсутствие разброса точек корреляционного поля вокруг выборочной линии регрессии (рис. 3.11). То есть в этом случае каждому Xi соответствует лишь одно значение ![]() . Иначе говоря, в этом случае выборочные данные свидетельствуют в пользу того, что величина Y жестко (функционально) зависит от величины X.
. Иначе говоря, в этом случае выборочные данные свидетельствуют в пользу того, что величина Y жестко (функционально) зависит от величины X.
Если в формуле (5.22) заменить реальные условные средние ![]() на сглаживающие условные средние
на сглаживающие условные средние ![]() и возвести полученное выражение в квадрат, то получим так называемый Выборочный коэффициент детерминации
и возвести полученное выражение в квадрат, то получим так называемый Выборочный коэффициент детерминации ![]()
|
|
Он показывает долю, которую составляет дисперсия ![]() сглаживающих средних
сглаживающих средних ![]() по отношению к общей дисперсии
по отношению к общей дисперсии ![]() выборочных значений Yj Исследуемого признака Y. То есть он показывает долю общего изменения (вариации) величины Y, объясняемую подобранным сглаживающим уравнением регрессии
выборочных значений Yj Исследуемого признака Y. То есть он показывает долю общего изменения (вариации) величины Y, объясняемую подобранным сглаживающим уравнением регрессии ![]() . Его обычно выражают в процентах.
. Его обычно выражают в процентах.
Выборочное корреляционное отношение HYx не зависит, очевидно, от формы выбранного сглаживающего уравнения регрессии ![]() , ибо его величина определяется исключительно выборочными данными. А вот выборочный коэффициент детерминации Dyx От этой формы зависит. Как можно доказать,
, ибо его величина определяется исключительно выборочными данными. А вот выборочный коэффициент детерминации Dyx От этой формы зависит. Как можно доказать,
|
|
И чем больше Dyx (чем ближе он к ![]() ), тем лучше построенное сглаживающее уравнение регрессии объясняет вариацию (изменение) зависимой величины Y. А следовательно, тем удачнее это уравнение построено. При
), тем лучше построенное сглаживающее уравнение регрессии объясняет вариацию (изменение) зависимой величины Y. А следовательно, тем удачнее это уравнение построено. При ![]() сглаживающая линия регрессии
сглаживающая линия регрессии ![]() точно пройдет через все экспериментальные точки
точно пройдет через все экспериментальные точки ![]() корреляционного поля, то есть через все узлы ломаной, изображенной на рис. 3.11. Это – идеальный вариант для сглаживающей линии. Правда, уравнение
корреляционного поля, то есть через все узлы ломаной, изображенной на рис. 3.11. Это – идеальный вариант для сглаживающей линии. Правда, уравнение ![]() такой идеальной сглаживающей линии при большом числе узлов выборочной ломаной линии регрессии, как правило, слишком сложно. Поэтому на практике идут на существенное упрощение подбираемого сглаживающего уравнения регрессии, жертвуя при этом неизбежным снижением коэффициента детерминации. Если же усложнение сглаживающего уравнения регрессии не пугает, то среди различных подобранных сглаживающих уравнений лучшим считается то, которое обеспечивает наибольший коэффициент детерминации. На вычислительных машинах, кстати, и построение сглаживающих уравнений регрессии в различных формах, и выбор из них наилучшего (по коэффициенту детерминации) делается по специальной стандартной программе.
такой идеальной сглаживающей линии при большом числе узлов выборочной ломаной линии регрессии, как правило, слишком сложно. Поэтому на практике идут на существенное упрощение подбираемого сглаживающего уравнения регрессии, жертвуя при этом неизбежным снижением коэффициента детерминации. Если же усложнение сглаживающего уравнения регрессии не пугает, то среди различных подобранных сглаживающих уравнений лучшим считается то, которое обеспечивает наибольший коэффициент детерминации. На вычислительных машинах, кстати, и построение сглаживающих уравнений регрессии в различных формах, и выбор из них наилучшего (по коэффициенту детерминации) делается по специальной стандартной программе.
Кстати, если сглаживающее уравнение регрессии строить в линейной (наиболее простой) форме (5.5), то будем иметь:
|
|
Действительно, для этого случая на основании (5.16) имеем:
|
|
Если сглаживающее уравнение регрессии ![]() строится в нелинейной и достаточно сложной форме, то такое построение трудно произвести вручную, и его лучше поручить машине. Если же возможности воспользоваться машиной (персональным компьютером) нет, то для несложных нелинейных случаев, в частности для уравнений вида (5.6) и (5.7) все можно сделать и вручную. Делается это с помощью метода наименьших квадратов совершенно аналогично тому, как это было проделано выше при построении сглаживающего линейного уравнения (5.5), принявшего итоговую форму (5.16).
строится в нелинейной и достаточно сложной форме, то такое построение трудно произвести вручную, и его лучше поручить машине. Если же возможности воспользоваться машиной (персональным компьютером) нет, то для несложных нелинейных случаев, в частности для уравнений вида (5.6) и (5.7) все можно сделать и вручную. Делается это с помощью метода наименьших квадратов совершенно аналогично тому, как это было проделано выше при построении сглаживающего линейного уравнения (5.5), принявшего итоговую форму (5.16).
Пусть, например, сглаживающее уравнение регрессии строится в гиперболической форме (5.6). Заметим, что такое уравнение – это фактически уравнение (5.5), если в последнем заменить X На ![]() . Поэтому для параметров K И B Уравнения (5.6) мы можем воспользоваться формулами (5.15), заменив в них X На
. Поэтому для параметров K И B Уравнения (5.6) мы можем воспользоваться формулами (5.15), заменив в них X На ![]() :
:
|
|
Здесь
|
|
Наконец, рассмотрим еще построение сглаживающего уравнения регрессии в параболической форме (5.7). Формируя для этого случая сумму (5.9)
|
|
И отыскивая ее минимум, приходим к аналогичной (5.12) нормальной системе для нахождения параметров (A0; A1; A2) сглаживающего уравнения регрессии (5.7). Приведём окончательный вид этой системы:
|
|
Решая эту систему, находим (A0; A1; A2), а вместе с ними – и искомое параболическое уравнение регрессии (5.7).
Построив сглаживающее уравнение регрессии ![]() В нескольких различных формах (линейное, гиперболическое, параболическое и т. д.) и выбрав из них лучшее, мы тем не менее еще не можем быть уверены в пригодности такого уравнения для приближения им истинного (генерального) уравнения регрессии
В нескольких различных формах (линейное, гиперболическое, параболическое и т. д.) и выбрав из них лучшее, мы тем не менее еще не можем быть уверены в пригодности такого уравнения для приближения им истинного (генерального) уравнения регрессии ![]() . Дело в том, что построенная сглаживающая линия регрессии может на некоторых своих участках выходить за пределы корреляционного поля, особенно если полоса точек этого поля узкая (корреляционная зависимость Y От X близка к функциональной). Тогда на этих участках сглаживающая линия не будет соответствовать корреляционному полю (будем неадекватна ему), а значит, будет неадекватно ему и уравнение
. Дело в том, что построенная сглаживающая линия регрессии может на некоторых своих участках выходить за пределы корреляционного поля, особенно если полоса точек этого поля узкая (корреляционная зависимость Y От X близка к функциональной). Тогда на этих участках сглаживающая линия не будет соответствовать корреляционному полю (будем неадекватна ему), а значит, будет неадекватно ему и уравнение ![]() этой сглаживающей линии. Такое уравнение не может быть использовано для всех Х, входящих в корреляционную таблицу, а значит, его применение чревато грубыми ошибками, если им мы будем приближать генеральное уравнение регрессии
этой сглаживающей линии. Такое уравнение не может быть использовано для всех Х, входящих в корреляционную таблицу, а значит, его применение чревато грубыми ошибками, если им мы будем приближать генеральное уравнение регрессии ![]() . В этом случае уравнение
. В этом случае уравнение ![]() считается Неадекватным выборочным данным И применяться не должно.
считается Неадекватным выборочным данным И применяться не должно.
Таким образом, после построения сглаживающего уравнения регрессии ![]() его еще нужно проверить на адекватность выборочным данным. Адекватность этого уравнения будет тем выше, чем лучше будет соответствующая ему сглаживающая линия регрессии вписываться в полосу точек корреляционного поля. То есть чем меньше будет разброс этих точек вокруг указанной линии.
его еще нужно проверить на адекватность выборочным данным. Адекватность этого уравнения будет тем выше, чем лучше будет соответствующая ему сглаживающая линия регрессии вписываться в полосу точек корреляционного поля. То есть чем меньше будет разброс этих точек вокруг указанной линии.
Оценим величину этого разброса. Для этого подсчитаем сумму квадратов отклонений ординат Yi Всех точек корреляционного поля от сглаживающей линии регрессии ![]() :
:
|
|
Проведем следующее преобразование этой суммы:

![]()
Учитывая, согласно (5.2) и (5.3), что
![]()
Получим окончательно:
|
Q0 = QПовт + QАдекв (5.32) |
Здесь
|
|
Сумма QПовт характеризует разброс выборочных значений ![]() вокруг выборочных средних
вокруг выборочных средних ![]() при проведении повторных опытов для различных Xi, поэтому она так и обозначена: QПовт. Она определяет степень влияния на величину Y различных неучтенных факторов (помех), не связанных с величиной Х. Кстати, сумма QПовт Не зависит, очевидно, от сглаживающего уравнения регрессии
при проведении повторных опытов для различных Xi, поэтому она так и обозначена: QПовт. Она определяет степень влияния на величину Y различных неучтенных факторов (помех), не связанных с величиной Х. Кстати, сумма QПовт Не зависит, очевидно, от сглаживающего уравнения регрессии ![]() , так что уменьшить или увеличить ее нельзя – она определяется исключительно выборочными данными. А вот вторая сумма QАдекв зависит от вида уравнения
, так что уменьшить или увеличить ее нельзя – она определяется исключительно выборочными данными. А вот вторая сумма QАдекв зависит от вида уравнения ![]() . Она характеризует меру отклонений сглаживающих средних
. Она характеризует меру отклонений сглаживающих средних ![]() от реальных (выборочных) средний
от реальных (выборочных) средний ![]() . И чем эта сумма меньше, тем более адекватным будет, очевидно, сглаживающее уравнение регрессии
. И чем эта сумма меньше, тем более адекватным будет, очевидно, сглаживающее уравнение регрессии ![]() . Поэтому эта сумма так и обозначена: QАдекв. Кстати, сумма QАдекв – это как раз та сумма Q (см. (5.9)), на минимизации которой основано построение сглаживающего уравнения регрессии.
. Поэтому эта сумма так и обозначена: QАдекв. Кстати, сумма QАдекв – это как раз та сумма Q (см. (5.9)), на минимизации которой основано построение сглаживающего уравнения регрессии.
Естественно, что если QАдекв = 0, то сглаживающее уравнение регрессии полностью адекватно выборочным данным (корреляционной таблице (5.1)). А если QАдекв ¹ 0, что обычно и бывает на самом деле, то сравнивая QАдекв С QПовт выясняют, достаточно ли мала сумма QАдекв, чтобы для данного уровня значимости A можно было бы принять нулевую гипотезу Н0 об адекватности сглаживающего уравнения регрессии ![]() при альтернативной гипотезе Н1 Об его неадекватности. Это можно сделать по критерию Фишера-Снедекора, если заведомо известно (или подтверждено экспериментально), что зависимая случайная величина Y при любом значении Х величины Х распределена по нормальному закону и имеет не зависящую от Х постоянную дисперсию.
при альтернативной гипотезе Н1 Об его неадекватности. Это можно сделать по критерию Фишера-Снедекора, если заведомо известно (или подтверждено экспериментально), что зависимая случайная величина Y при любом значении Х величины Х распределена по нормальному закону и имеет не зависящую от Х постоянную дисперсию.
Для этого делением сумм QПовт И QАдекв. на соответствующие им числа степеней свободы KПовт = N – N и KАдекв. = N – Q (Q – число коэффициентов уравнения регрессии) находят дисперсию повторности ![]() и дисперсию адекватности
и дисперсию адекватности ![]()
|
|
После этого находят выборочное значение критерия F Фишера-Снедекора
|
|
И сравнивают его с критическим значением
![]() , (5.36)
, (5.36)
взятом из таблицы 5 Приложения. И если FВыб > FКр, то при данном уровне значимости A гипотезу Н0 об адекватности сглаживающего уравнения регрессии отвергают. То есть считают подобранное уравнение ![]() непригодным для приближения истинного (генерального) уравнения регрессии
непригодным для приближения истинного (генерального) уравнения регрессии ![]() . А если окажется, что FВыб < FКр, то нет оснований отвергать гипотезу Н0. И только такое (адекватное) уравнение регрессии можно использовать в дальнейшем.
. А если окажется, что FВыб < FКр, то нет оснований отвергать гипотезу Н0. И только такое (адекватное) уравнение регрессии можно использовать в дальнейшем.
Кстати, если для имеющихся выборочных данных построено несколько различных сглаживающих выборочных уравнений регрессии, и все они адекватны выборочным данным, то лучшим среди них считается то, которое, не являясь заметно сложнее прочих, обеспечивает наибольший коэффициент детерминации ![]() .
.
Наряду с проверкой адекватности сглаживающего уравнения регрессии имеется возможность проверить и Значимость каждого его коэффициента в отдельности. Это значит – имеется возможность установить, достаточно ли подсчитанное значение интересующего нас коэффициента для статистически обоснованного вывода а том, что он отличен от нуля. И если окажется, что коэффициент не значим, то его можно положить равным нулю. Это приведет к упрощению сглаживающего уравнения регрессии без существенного ущерба для его качества. Но на этом мы не останавливаемся. Отметим лишь, что такое исследование производится автоматически, если сглаживающее уравнение регрессии строится с помощью стандартной программы корреляционно-регрессионного анализа на ЭВМ. В сглаживающем уравнении регрессии, выдаваемом машиной, фигурируют лишь значимые коэффициенты, а заодно и указывается, адекватно ли все уравнение в целом.
Пример 1. На некотором предприятии исследовалась зависимость себестоимости Y единицы продукции (в условных единицах) от объема Х Произведенной за день продукции. Статистическое распределение выборки за 30 рабочих дней приведено в следующей таблице:
|
Xi yj |
5 |
10 |
15 |
20 |
25 |
|
(5.37) |
|
10 |
– |
– |
– |
1 |
4 |
5 | |
|
11 |
– |
3 |
6 |
4 |
1 |
14 | |
|
12 |
1 |
3 |
2 |
– |
1 |
7 | |
|
13 |
3 |
– |
1 |
– |
– |
4 | |
|
|
4 |
6 |
9 |
5 |
6 |
N = 30 |
Требуется подобрать подходящую форму сглаживающего уравнения регрессии ![]() , оценивающего корреляционную зависимость себестоимости Y единицы продукции от объема Х продукции, произведенной за день, и построить это уравнение. Оценить степень тесноты указанной корреляционной зависимости, а также качество и адекватность построенного сглаживающего уравнения регрессии.
, оценивающего корреляционную зависимость себестоимости Y единицы продукции от объема Х продукции, произведенной за день, и построить это уравнение. Оценить степень тесноты указанной корреляционной зависимости, а также качество и адекватность построенного сглаживающего уравнения регрессии.
Решение. Сначала по данным корреляционной таблицы (5.37) построим
 |
 Корреляционное поле (рис. 3.13.).
Корреляционное поле (рис. 3.13.).
Рис. 3.13
Используя формулу (5.3), вычислим для каждого ![]() выборочную среднюю
выборочную среднюю ![]() :
:
![]()
![]()
![]()
![]()
![]()
По точкам (![]() ) строим на корреляционном поле выборочную линию регрессии – ломанную L (ее узлы на рис. 3.13 обозначены квадратиками).
) строим на корреляционном поле выборочную линию регрессии – ломанную L (ее узлы на рис. 3.13 обозначены квадратиками).
Теперь встает очередная задача – в какой форме ![]() искать сглаживающее равнение этой выборочной линии регрессии?
искать сглаживающее равнение этой выборочной линии регрессии?
Обратим внимание на то, что с увеличением X выборочные средние ![]() убывают, причем это убывание затухает. Так и должно быть (по смыслу рассматриваемых величин X и Y). Это дает основание строить сглаживающее выборочное уравнение регрессии в гиперболической форме (5.6). Коэффициенты K и B этого уравнения находятся по данным корреляционной таблицы (5.37) с помощью формул (5.27) и (5.28):
убывают, причем это убывание затухает. Так и должно быть (по смыслу рассматриваемых величин X и Y). Это дает основание строить сглаживающее выборочное уравнение регрессии в гиперболической форме (5.6). Коэффициенты K и B этого уравнения находятся по данным корреляционной таблицы (5.37) с помощью формул (5.27) и (5.28):
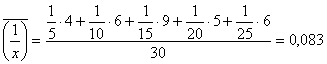
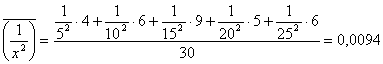
![]() (5.39)
(5.39)
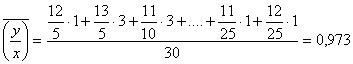
![]()
![]()
Итак, сглаживающее выборочное уравнение регрессии в гиперболической форме (5.6) таково:
![]() (5.40)
(5.40)
Вычислим сглаживающие средние ![]() для всех Xi и сравним их с реальными выборочными средними
для всех Xi и сравним их с реальными выборочными средними ![]() :
:
|
Xi |
5 |
10 |
15 |
20 |
25 |
(5.41) |
|
Ni |
4 |
6 |
9 |
5 |
6 | |
|
|
12,75 |
11,50 |
11,44 |
10,80 |
10,50 | |
|
|
12,85 |
11,55 |
11,12 |
10,90 |
10,77 |
Впрочем, сначала убедимся, что и те, и другие средние подсчитаны правильно. Используя в качестве контроля формулы (5.10) убеждаемся, что обе суммы (5.10) дают один и тот же результат – общую среднюю ![]() =11,33. То есть и реальные, и сглаживающие средние подсчитаны верно. И они весьма близки друг к другу. Это демонстрирует и рис. 3.13, где изображена гипербола (5.40) с указанием на ней точек
=11,33. То есть и реальные, и сглаживающие средние подсчитаны верно. И они весьма близки друг к другу. Это демонстрирует и рис. 3.13, где изображена гипербола (5.40) с указанием на ней точек ![]() , помеченных треугольниками.
, помеченных треугольниками.
А теперь перейдем к получению ответов на остальные вопросы – о степени тесноты корреляционной зависимости Y от X и о качестве построенного уравнения (5.40).
Степень тесноты корреляционной зависимости Y от X оценивает выборочное корреляционное отношение ![]() .
.![]() Подсчитывая его по формуле (5.22), получим:
Подсчитывая его по формуле (5.22), получим: ![]() . Величина
. Величина ![]() Оказалась весьма значительной (гораздо ближе к 1, чем нулю), что указывает на определенную и достаточно тесную корреляционную зависимость Y от X.
Оказалась весьма значительной (гораздо ближе к 1, чем нулю), что указывает на определенную и достаточно тесную корреляционную зависимость Y от X.
Подсчитаем еще, используя формулу (5.23), выборочный коэффициент детерминации ![]()
![]() . При этом, согласно (5.24),
. При этом, согласно (5.24),
![]() (5.42)
(5.42)
Значение ![]() указывает, что построенное сглаживающее выборочное уравнение регрессии (5.40) объясняет 52% общего объема вариации (изменения) величины Y в выборке и лишь немного не дотягивает до своего максимально возможного значения в 56,25 %. И это имеет место при весьма простом виде уравнения (5.40). Чтобы окончательно убедиться в высоком качестве этого уравнения, следует проверить его на адекватность выборочным данным. Для этого, используя формулы (5.33) – (5.35), подсчитаем выборочное значение критерия Фишера – Снедекора:
указывает, что построенное сглаживающее выборочное уравнение регрессии (5.40) объясняет 52% общего объема вариации (изменения) величины Y в выборке и лишь немного не дотягивает до своего максимально возможного значения в 56,25 %. И это имеет место при весьма простом виде уравнения (5.40). Чтобы окончательно убедиться в высоком качестве этого уравнения, следует проверить его на адекватность выборочным данным. Для этого, используя формулы (5.33) – (5.35), подсчитаем выборочное значение критерия Фишера – Снедекора:
![]()
![]()
![]()
![]()
![]() (5.43)
(5.43)
Далее задаем уровень значимости ![]() (например
(например ![]() =0,05) и по таблице критических точек распределения Фишера – Снедекора находим:
=0,05) и по таблице критических точек распределения Фишера – Снедекора находим:
![]() (5.44)
(5.44)
И так как оказалось, что ![]() , то у нас нет оснований отвергать гипотезу Н0 об адекватности уравнения (5.40) выборочным данным. В пользу этого свидетельствует и рис. 3.13: гипербола L* нигде не выходит за пределы корреляционного поля.
, то у нас нет оснований отвергать гипотезу Н0 об адекватности уравнения (5.40) выборочным данным. В пользу этого свидетельствует и рис. 3.13: гипербола L* нигде не выходит за пределы корреляционного поля.
Все задания примера 1 выполнены.
Кстати, если бы мы искали сглаживающее выборочное уравнение регрессии в линейной форме (5.5), то, используя (5.13) и (5.15), получили бы:
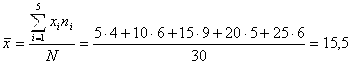
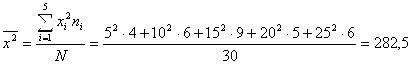

![]()
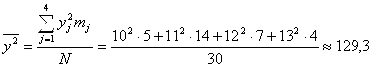
![]()
![]()
![]()
![]()
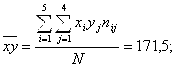
![]()
И тогда вместо гиперболического (5.40) мы бы получили линейное уравнение
![]() (5.46)
(5.46)
Если подсчитать по этому уравнению сглаживающие средние ![]() и сравнить их с реальными выборочными средними
и сравнить их с реальными выборочными средними ![]() , то получим следующую таблицу:
, то получим следующую таблицу:
|
Xi |
5 |
10 |
15 |
20 |
25 |
(5.47) |
|
Ni |
4 |
6 |
9 |
5 |
6 | |
|
|
12,75 |
11,50 |
11,44 |
10,80 |
10,50 | |
|
|
12,37 |
11,87 |
11,38 |
10,89 |
10,40 |
Если для полученных сглаживающих средних ![]() провести, на основе формулы (5.10), контроль, то он (проверьте это) сходится - опять получаем общую среднюю
провести, на основе формулы (5.10), контроль, то он (проверьте это) сходится - опять получаем общую среднюю ![]() .
.
Как видим, в таблице (5.47), как и в таблице (5.41), расхождение средних ![]() И
И ![]() невелико. То есть линейное уравнение (5.46), как и гиперболическое уравнение (5.40), тоже достаточно качественное.
невелико. То есть линейное уравнение (5.46), как и гиперболическое уравнение (5.40), тоже достаточно качественное.
Выясним все же, какое из них лучше. Для этого подсчитаем выборочный коэффициент детерминации DyХ и для линейного уравнения (5.46) . Используя формулу (5.23) получим: DyХ![]() =50%. Впрочем, в линейном случае его можно было бы найти и по формуле (5.26), если предварительно найти выборочный коэффициент линейной корреляции
=50%. Впрочем, в линейном случае его можно было бы найти и по формуле (5.26), если предварительно найти выборочный коэффициент линейной корреляции ![]() :
:
![]()
![]()
Итак, линейное сглаживающее уравнение регрессии (5.46) объясняет примерно 50% всей вариации зависимой величины Y. Гиперболическое же уравнение (5.40) объясняло чуть больше – 52% этой вариации. То есть по этому показателю гиперболическое уравнение несколько лучше линейного. И оно, по существу, так же просто, как и линейное.
Выше мы показали, что гиперболическое уравнение адекватно выборочным данным. Покажем, что и линейное уравнение им адекватно. Используя опять формулы (5.33) – (5.35), получаем:
![]() (см. (5.43)
(см. (5.43)
![]() (5.49)
(5.49)
![]()
![]()
![]()
При том же уровне значимости ![]() =0,05, который был принят при проверке гипотезы об адекватности гиперболического уравнения регрессии, в соответствии с (5.36) получаем для линейного уравнения (5.46) то же самое критическое значение критерия Фишера – Снедекора, что было указано в (5.44):
=0,05, который был принят при проверке гипотезы об адекватности гиперболического уравнения регрессии, в соответствии с (5.36) получаем для линейного уравнения (5.46) то же самое критическое значение критерия Фишера – Снедекора, что было указано в (5.44): ![]() . И так как опять
. И так как опять ![]() , то у нас нет оснований отвергать гипотезу Н0 И об адекватности линейного сглаживания уравнения регрессии (5.46) выборочным данным.
, то у нас нет оснований отвергать гипотезу Н0 И об адекватности линейного сглаживания уравнения регрессии (5.46) выборочным данным.
В общем, оба сглаживающие выборочные уравнения регрессии – гиперболическое (5.40) и линейное (5.46) – адекватны выборочным данным и оба достаточно хороши. Из них несколько лучшим является гиперболическое уравнение (5.40).
| < Предыдущая | Следующая > |
|---|
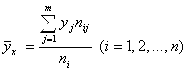 (5.3)
(5.3)


 (5.10)
(5.10) (5.11)
(5.11) (5.12)
(5.12) (5.13)
(5.13)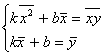 (5.14)
(5.14)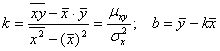 (5.15)
(5.15)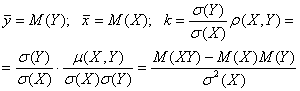 (5.17)
(5.17)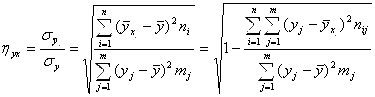 (5.22)
(5.22) (5.23)
(5.23) (5.26)
(5.26)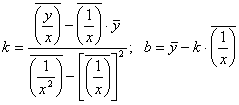 (5.27)
(5.27)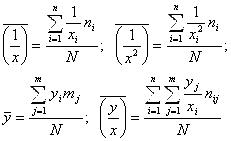 (5.28)
(5.28) (5.30)
(5.30)