2.07. Проверка гипотезы о равенстве математических ожиданий двух нормально распределенных случайных величин (большие независимые выборки)

Пусть X И Y – две независимые нормально распределенные случайные величины. Требуется с помощью выборочных данных, полученных при исследовании значений этих величин, проверить нулевую гипотезу H0 о равенстве этих математических ожиданий при альтернативной гипотезе H1 об их неравенстве. Такая задача, например, будет актуальной при выяснении вопроса о том, изготовляют ли два параллельно работающих станка одинаковые в среднем детали или все же разные. Или имеют два сорта сельскохозяйственной культуры одинаковую в среднем урожайность или все же разную.

Пусть и – объемы выборок, а и – выборочная средняя и исправленная выборочная дисперсия указанных выборок. Образуем случайную величину Z = -. При условии справедливости гипотезы H0 Случайная величина Z распределена нормально с

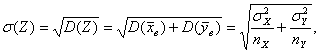(3.12)

Где и – истинные (генеральные) дисперсии величин X и Y. При заданном уровне значимости α областью принятии гипотезы H0 Будет, очевидна, интервал

(3.13)

Где находится из условия:

(3.14)

А это, на основании формулы (4.11) (часть I, глава 2), дает:

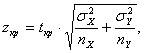где (3.15)

Генеральные дисперсии и обычно неизвестны. Но если объемы выборок и достаточно велики, то есть они не менее 30 (что мы и предполагаем для больших выборок), то в (3.15) можно заменить и их точечными оценками и .

Пример 3. По двум независимым выборкам объемами =100 и =120 найдены выборочные средние = 32,4 и = 30,1, а также исправленные выборочные дисперсии =15,0 и =25,2. Исследуемые с помощью этих выборок случайные величины X и Y распределены нормально. При уровне значимости α = 0,05 проверить нулевую гипотезу H0 о том, что M(X) = M(Y) при альтернативной гипотезе H1 о том, что M(X) ≠ M(Y).

Решение. Находим сначала опытное (экспериментальное) значение ZЭксп нормально распределенной величины Z = - :

ZЭксп = - = 32,4 - 30,1 = 2,3

Далее из равенства с помощью таблицы интеграла вероятности Ф(X) находим TКр: TКр =1,96. После этого по формуле (3.15) вычисляем : =1,176. Таким образом, интервалом принятия гипотезы Н0 Для значений величины Z будет следующий интервал:

= (-1,176; 1,176)

Так как экспериментальное значение ZЭксп = 2,3 величины Z не входит в этот интервал, то гипотезу Н 0 о равенстве математических ожиданий величин X и Y отвергаем – она не подтверждается экспериментальными данными.

< Предыдущая		Следующая >