2.08. Проверка гипотезы о равенстве математических ожиданий двух нормально распределенных случайных величин (малые независимые выборки)

Рассмотрим ту же задачу, что и в предыдущем пункте 3.4, но только при условии, что объемы выборок и Невелики (меньше 30). В этом случае замена генеральных дисперсий и , входящих в (3.15), на исправленные выборочные дисперсии и может привести к большой ошибке в величине , а следовательно, к большой ошибке в установлении области принятия гипотезы Н0. Однако если есть уверенность в том, что неизвестные генеральные и Одинаковы (например, если сравниваются средние размеры двух партий деталей, изготовленных на одном и том же станке), то можно, используя распределение Стьюдента, и в этом случае построить критерий проверки гипотезы Н0 о равенстве математических ожиданий величин X и Y. Для этого вводят случайную величину

, (3.16)

Где

(3.17)

- среднее из исправленных выборочных дисперсий и , служащее точечной оценкой обеих одинаковых неизвестных генеральных дисперсий и . Как оказывается (см. [3], стр.180), при справедливости нулевой гипотезы Н0 случайная величина Т имеет распределение Стьюдента с степенями свободы независимо от величин и объемов выборок. Если гипотеза Н0 верна, то разница должна быть невелика. То есть экспериментальное значение TЭксп. величины Т должно быть невелико. А именно, должно заключаться в некоторых границах . Выход же его за эти границы мы будем считать опровержением гипотезы Н0, и допускать это будем с вероятностью, равной задаваемому уровню значимости α.

Таким образом, областью принятия гипотезы Н0 будет являться некоторый интервал , в который значения случайной величины Т должны попадать с вероятностью 1- α:

(3.18)

Величину , определяемую равенством (3.18), для различных уровней значимости α и различных числах K степеней свободы величины Т можно найти в таблице критических точек распределения Стьюдента (таблице 4 Приложения). Тем самым будет найден интервал принятия гипотезы Н0. И если экспериментальное значение TЭксп величины Т попадет в этот интервал – гипотезу Н0 принимают. Не попадает - не принимают.

Примечание 1. Если нет оснований считать равными генеральные дисперсии и величин Х и Y, то и в этом случае для проверки гипотезы Н0 о равенстве математических ожиданий величин Х и Y допускается использование изложенного выше критерия Стьюдента. Только теперь у величины Т число K степеней свободы следует считать равным не , а равным (см. [1])

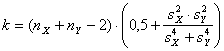(3.19)

Если исправленные выборочные дисперсии и различаются существенно, то второе слагаемое в последней скобке (3.19) невелико по сравнению с 0,5, так что выражение (3.19) по сравнению с выражением уменьшает число степеней свободы случайной величины Т почти вдвое. А это ведет к существенному расширению интервала принятия гипотезы Н0 и, соответственно, к существенному сужению критической области непринятия этой гипотезы. И это вполне справедливо, так как степень разброса возможных значений разности Будет, в основном, определяться разбросом значений той из величин Х и Y, которая имеет большую дисперсию. То есть информация от выборки с меньшей дисперсией как бы пропадает, что и ведет к большей неопределенности в выводах о гипотезе Н0 .

Пример 4. По приведенным в таблице данным сравнить средние удои коров, получавших различные рационы. При проверке нулевой гипотезы Н0 о равенстве средних удоев принять уровень значимости α=0,05.

Рацион	Поголовье коров, получавших рацион (Голов)	Среднесуточный удой в пересчете на базисную жирность (Кг/на голову)	Среднеквадратическое отклонение суточной молочной продуктивности коров (Кг/на голову)
№ 1	10 ()	16,2 ()	3,8 ()
№ 2	8 ()	17,7 ()	4,2 ()

Решение. Так как приведенные табличные данные получены на основании малых выборок объемами =10 и =8, то для сравнения математических ожиданий среднесуточных удоев коров, получавших тот и другой кормовые рационы, мы должны использовать теорию, изложенную в этом пункте. Для этого в первую очередь выясним, позволяют ли найденные исправленные выборочные дисперсии =(3,8)2=14,44 и =(4,2)2=17,64 считать равными генеральные дисперсии и . Для этого используем критерий Фишера-Снедекора (см. пункт 3.3). Имеем:

По таблице критических точек распределения Фишера-Снедекора для α=0,05; K1=8-1=7 и K2=10-1=9 находим

И так как , то у нас нет оснований при данном уровне значимости α=0,05 отвергать гипотезу H0 о равенстве генеральных дисперсий и .

Теперь, в соответствии с (3.17) и (3.16), подсчитаем экспериментальное значение величины Т:

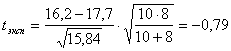
Далее, по формуле находим число K степеней свободы величины Т: K=10+8-2=16. После этого для п0+8-2=16. ооды (3.16) подсчитаем экспериментальное значение величины Т: Ы кормовые рационы, мы должны испол α=0,05 и K=16 по таблице критических точек распределения Стьюдента (таблица 4 Приложения) находим : =2,12. Таким образом, интервалом принятия гипотезы H0 о равенстве средних удоев коров, получавших рационы № 1 и № 2, является интервал =(-2,12; 2,12). И так как = - 0,79 попадает в этот интервал, то у нас нет оснований отвергать гипотезу H0. То есть мы вправе считать, что различие кормовых рационов не сказывается на среднесуточном удое коров.

Примечание 2. В рассмотренных выше пунктах 3.4 и 3.5 рассматривалась нулевая гипотеза H0 о равенстве М(Х)=М(Y) при альтернативной гипотезе Н1 об их неравенстве: М(Х)≠М(Y). Но альтернативная гипотеза Н1 может быть и другой, например, М(Y)>М(X). На практике этот случай будет иметь место, когда вводится некоторое усовершенствование (положительный фактор), который позволяет рассчитывать на увеличение в среднем значений нормально распределенной случайной величины Y по сравнению со значениями нормально распределенной величины Х. Например, в рацион коров введена новая кормовая добавка, позволяющая рассчитывать на увеличение среднего удоя коров; под культуру внесена дополнительная подкормка, позволяющая рассчитывать на увеличение средней урожайности культуры, и т. д. И хотелось бы выяснить, существенен (значим) или незначим этот введенный фактор. Тогда в случае больших объемов и Выборок (см. пункт 3.4) в качестве критерия справедливости гипотезы H0 рассматривают нормально распределенную случайную величину

(3.20)

При заданном уровне значимости α Гипотеза H0 о равенстве М(Х) и М(Y) будет отвергнута, если экспериментальное значение величины Будет положительным и бόльшим , где

(3.21)

Так как при справедливости гипотезы H0 М(Z)=0, то

(3.22)

Откуда следует:

то есть (3.23)

Из последнего равенства по таблице интеграла вероятностей Ф(х) находится , а затем, по первой из формул (3.15), находится критическое значение величины . И если экспериментальное значение этой величины больше - гипотезу H0 О равенстве М(Х) и М(Y) отвергают, утверждая тем самым существенность (значимость) нововведенного фактора. А если окажется, что < , то этот фактор признается незначимым.

Аналогичное видоизменение претерпит проверка гипотезы H0: М(Х)=М(Y) при альтернативной гипотезе Н1: М(Y)>М(X) и в случае малых выборок (пункт 3.5). В качестве критерия проверки гипотезы H0 Вводят величину

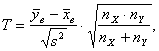(3.24)

Имеющую, при справедливости гипотезы H0 И при равенстве дисперсий и , распределение Стьюдента с тем же числом степеней свободы , что и в пункте 3.5. Гипотеза H0 будет отвергнута, если экспериментальное значение величины Т окажется положительным и достаточно большим (>), где найдется по таблице критических точек распределения Стьюдента из равенства

, (3.25)

Представляющего собой аналог равенства (3.18). Действительно, так как распределение Стьюдента симметрично относительно точки T=0, то

(3.26)

Или

, (3.27)

Откуда и следует равенство (3.25).

< Предыдущая		Следующая >