2.06. Проверка гипотезы о равенстве дисперсий двух нормально распределенных случайных величин

Гипотезы о дисперсиях имеют особенно большое значение в технике, так как дисперсия характеризует рассеяние значений случайной величины вокруг среднего значения этой величины. А значит, в технике она характеризует точность измерительных приборов, устойчивость работы машин, отлаженность технологических процессов, и т. д. Очевидно, предпочтительнее тот прибор, инструмент или процесс, который обеспечивает наименьшее рассеяние результатов измерений или действий. То есть обеспечивает наименьшую дисперсию.

Пусть X и Y – две нормально распределенные случайные величины, имеющие одно и то же наименование (размерность). Например, пусть Х - результат измерения некоторой величины одним прибором, а Y – результат измерения этой же (или какой-то другой) величины той же размерности, что и первая, другим прибором. Параметры (; ) и (; ) этих нормально распределенных случайных величин будем считать неизвестными. То есть нам не известны ни истинные значения и измеряемых приборами величин, ни точности и приборов. Требуется при заданном уровне значимости α проверить нулевую гипотезу H0 о том, что дисперсии величин X и Y, а значит и точность обоих приборов, одинаковы: =. В качестве альтернативной гипотезы H1 примем гипотезу, состоящую в том, что прибор, который на практике оказался менее точным (показал больший разброс результатов измерений) и на самом деле является менее точным.

Для статистической проверки нулевой гипотезы H0 произведем и повторных измерений величин X и Y, и по полученным выборочным данным найдем исправленные выборочные дисперсии и . Эти исправленные выборочные дисперсии являются, как мы знаем, точечными несмещенными оценками истинных дисперсий и величин X и Y:

≈ ; ≈ (3.7)

Таким образом, сравнение и сводится к сравнению и . Если окажется, что = (что маловероятно из-за случайности выборок), то гипотеза H0, естественно, считается принятой. Но обычно ≠ . И поэтому возникает вопрос: существенно ли (значимо) или несущественно (незначимо) отличается бόльшая из них от меньшей? То есть принимать ли гипотезу H0 о равенстве дисперсий и , а значит, и о равной точности обоих приборов? Или все же склониться в сторону альтернативной гипотезы H1 о том, что один из приборов точнее другого?

Для решения этого вопроса введем случайную величину F, представляющую собой отношение бόльшей исправленной дисперсии к меньшей:

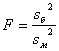(3.8)

(F – случайная величина, так как и – сами случайные величины). Доказано, что при условии справедливости гипотезы H0 О равенстве и введенная случайная величина F имеет распределение Фишера-Снедекора (см. §4, глава 2) со степенями свободы K1 = N1-1 и K2 = N2 -1, где N1 – объем выборки c большей исправленной дисперсий, а N2 – с меньшей. Напомним, что распределение Фишера-Снедекора зависит только от степеней свободы K1 И K2 и не зависит от других параметров.

Ясно, что при справедливости гипотезы H0, утверждающей, что = , должны быть примерно равны и , так что экспериментальное значение

(3.9)

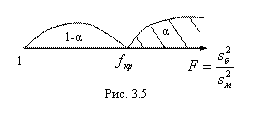Величины F не должно существенно превосходить единицу. То есть не должно превосходить некоторое значение FКр, где FКр > 1 (рис 3.5). Если оно его все же превзойдет, то это будет свидетельствовать о неправомерности принятия нулевой гипотезы H0. То есть если окажется, что FЭксп. > FКр., то мы гипотезу H0 Отвергнем.

Но если эта гипотеза все же верна, то отвергая её, мы совершим ошибку первого рода. Вероятность этой ошибки должна быть равна задаваемому уровню значимости α. А значит, для значения FКр получаем следующее равенство:

(3.10)

Или что одно и то же:

(3.11)

Величину FКр = FКр (α ; K1 ; K2) для заданных (α ; K1 ; K2) можно найти но специальной таблице критических точек распределения Фишера-Снедекора (см. таблицу 5 Приложения). И если окажется, что экспериментальное значение (3.9) величины F Окажется больше FКр (попадет в критическую область), то гипотезу H0 о равенстве двух дисперсий (о равной точности двух приборов) отвергают, принимая тем самым альтернативную гипотезу H1, о том, что один из приборов (с большей исправленной дисперсией) менее точен. А если окажется, что FЭксп < FКр (то есть если FЭксп попадет в область принятия гипотезы H0), то эту гипотезу H0 о равной точности обоих приборов принимают. Принимают, считая тем самым несущественным (незначимым) то различие исправленных дисперсий и , которое имеет место в проведенных двух сериях измерений этими приборами.

Пример 2. На двух токарных станках обрабатывается втулки. Отобраны две пробы: N1 = 10 штук - из втулок, обработанных на первом станке, и N2 = 15 штук - из втулок, обработанных на втором станке. По данным этих выборок найдены исправленные выборочные дисперсии: = 9,6 и = 5,7. Проверить при уровне значимости: а) α = 0.05 и б) α = 0,01 гипотезу H0 об одинаковой точности этих двух станков при альтернативной гипотезе H1 о том, что второй станок точнее, чем первый.

Решение. Здесь

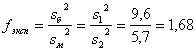
По таблице критических точек распределения Фишера – Снедекора (таблица 5 Приложения) для K1 = 10 – 1 = 9; K2 = 15 – 1 = 14 и а) α = 0,05; б) α = 0.01 находим FКр:

А) FКр = FКр (0,05; 9; 14) = 2,65;

Б) FКр = FКр (0,01; 9; 14) = 4,03.

Так как и в варианте (a), и варианте (б) FЭксп < FКр, то в обоих вариантах у нас нет оснований отвергать гипотезу H0 о равенстве дисперсий размеров втулок, обрабатываемых на обоих станках. То есть гипотеза H0 об одинаковой точности этих двух станков принимается. Тем самым имеющееся различие между и признается несущественным (незначимым) и относится на счет случайности проведенных выборок.

Примечание. Полученный вывод о незначимости различия выборочных дисперсий = 9,6 и = 5,7 получился, скорее всего, лишь из – за малости обеих выборок (N1 = 10 и N2 = 15). Если бы такие же значения и получились для больших выборок, то такое существенное различие между и было бы трудно объяснить случайностями самих выборок, и гипотеза H0 о равной точности станков была бы отвергнута. Действительно, согласно таблице 5 Приложения при K1 = N1 – 1 → ∞ и K2 = N2 – 1 → ∞ значение

FКр = FКр (α;K1;K2) → 1

При всех уровнях значимости α. Поэтому при больших значениях K1 и K2 было бы FЭксп > FКр, и гипотеза H0 Была бы отвергнута и в варианте (а), и в варианте (б).

< Предыдущая		Следующая >