2.05. Проверка гипотезы о значении математического ожидания нормально распределенной случайной величины

Пусть нулевая гипотеза H0 состоит в том, что математическое ожидание A нормальной распределенной случайной величины X равно некоторому заданному значению A0. А альтернативной гипотезой H1 является гипотеза о том, что A ≠ A0. Будем при этом пока предполагать, что параметр (среднее квадратическое отклонение величины X) известен. Такая задача будет, например, актуальной для станка-автомата, изготавливающего в массовом количестве некоторые детали, размер A0 которых задан. Если станок настроен правильно, то размер X изготавливаемых им деталей будет случайной величиной, распределенной нормально с известным математическим ожиданием A = A0 И известным средним квадратическим отклонением , определяемым классом точности станка. Но если станок настроен неправильно, у него будет A ≠ A0. Отобрав из продукции станка некоторую совокупность деталей и обмерив их, можно попытаться узнать, верна ли гипотеза H0 о том, что A=A0, или она должна быть отклонена в пользу альтернативной гипотезы H1, утверждающей, что A ≠ A0.

Итак, гипотеза H0­ сформулирована. Попробуем найти критерий ее правильности или неправильности.

Пусть выборочная средняя , являющаяся точечной оценкой генеральной средней = A, из выборки найдена. Предположим, что гипотеза H0 верна, то есть что = A = A0. В качестве случайной величины K, с помощью которой будем проверять гипотезу H0, возьмем нормально распределенную случайную величину K = - A0, математическое ожидание которой, если верна гипотеза H0, равно нулю. Выберем некоторый уровень значимости α. Если гипотеза H0 верна, то отклонение K = - A0 от нуля должно быть невелико, то есть практически должно находится в некоторых границах (-KКр; KКр). А выход его за эти границы следует считать опровержением гипотезы H0. То есть оставшиеся вне интервала (-KКр; KКр) участки числовой оси ОK Мы будем считать критической областью – областью непринятия гипотезы H0. При условии справедливости H0 ее непринятие – это ошибка первого рода. Поэтому вероятность попадания значения K Величины K = - A0 в критическую область должна быть равна вероятности совершить ошибку первого рода, то есть должна равняться принятому уровню значимости α. А вероятность попадания значения K в область (-KКр; KКр) принятия гипотезы H0 тогда должна быть равна γ = 1-α (см. рис. 3.4).

Очевидно, что чем меньше будет выбран уровень значимости α, то есть чем меньшей будет установлена вероятность совершить ошибку первого рода – отвергнуть нулевую гипотезу Н0, если она верна, тем шире должен быть интервал (-KКр; KКр) принятия этой гипотезы. При α = 0 должна быть вообще исключена возможность отвергнуть проверяемую гипотезу H0, если она верна. Но тогда в любом случае ее нужно принять. А это будет, согласно рис. 3.4, если заштрихованной области непринятия гипотезы H0 не будет вообще. То есть когда (-KКр; KКр) = (- ∞; ∞).

Итак, подведем итог. При заданном α ≠ 0 гипотеза Н0 должна быть отвергнута, если экспериментальное значение K=KЭксп нормально распределенной случайной величины К = - A0 Окажется вне интервала (-KКр; KКр). И она же может быть принята, если K=KЭксп попадет в интервал (-KКр; KКр).

Согласно рис. 3.4 имеем:

(3.2)

Сравнивая это равенство с равенством

, (3.2)

Вытекающем из равенства (2.22), если в последнем заменить на A0 и на , получим

, ( 3.3)

Откуда

, где (3.4)

После нахождения KКр находятся области принятия и непринятия гипотезы Н0:

1) Если KЭксп =- гипотезу H0 принимаем.

2) Если KЭксп =- гипотезу H0 отвергаем.

Примечание 1. Если неизвестно, то при достаточно большой выборке (N>30) можно заменить в приведенных выше формулах на её точечную оценку .

Примечание 2. Если неизвестно и выборка небольшая (N<30), то тогда в качестве критерия К проверки гипотезы Н0 используют случайную величину

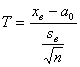, (3.5)

Имеющую распределение Стьюдента с K = N-1 степенями свободы (сравните с (2.27)). А областью принятия гипотезы Н0 считается интервал , в который с вероятностью γ = 1-α попадает экспериментальное значение TЭксп случайной величины Т :

(3.6)

Величину , соответствующую данным значениям α и K = N – 1, находят по таблице критических точек распределения Стьюдента (см. Приложение, таблица 4). Кстати, по этой же таблице по и K = N – 1 находят Tγ, входящее в равенство (2.28).

Примечание 3. В качестве гипотезы, альтернативной гипотезе H0, могла быть принята не гипотеза H1: A ≠ A0, А гипотеза H1: A > A0 Или гипотеза H1: A< A0. Тогда критическая область непринятия гипотезы H0 была бы не двусторонней, как на рис. 3.4, а односторонней с одной критической точкой KКр, определяемой соответственно неравенствами P(KКр <KЭксп <¥)=α или P(-¥<KЭксп < KКр)=α. Соответствующие изменения при проверке гипотезы H0 (а именно, при нахождении табличного значения KКр ) продумайте самостоятельно (или посмотрите ниже примечание 2 к пункту 3.5).

Пример 1. Выборочным путем исследовались 30 молочных пакетов, в которых, согласно их маркировке, должно содержаться 0,5 л. = 500 мл. молока. Получено следующее статистическое распределение выборки:

ХI (мл.)	480 – 490	490 – 500	500 – 510	510 – 520
Ni	8	10	8	4

Проверить при уровне значимости α = 0,05 нулевую гипотезу H0 о том, что автомат, заполняющий пакеты, настроен правильно (на норму 500 мл.), при альтернативной гипотезе H1, что станок настроен неправильно.

Решение. Пусть X (мл.) – реальное количество молока в пакете (X – случайная величина). Различие её значений для разных пакетов связано с действием большого числа случайных факторов, поэтому по теореме Ляпунова (глава 2, §4) можно считать, что она распределена нормально с некоторыми параметрами A = M (X) и σ = σ (X). Если гипотеза H0 верна (автомат настроен правильно), то A = 500 мл. А если гипотеза H0 неверна, то верна альтернативная гипотеза H1: A ≠ 500 мл.

Найдем числовые характеристики выборки – выборочную среднюю и выборочную дисперсию . Для этого сначала приведем статистическое распределение выборки от интервального вида к дискретному:

ХI (мл.)	485	495	505	515
Ni	8	10	8	4

Используя теперь формулы (1.5) – (1.7), получим:

≈ 497,7; ≈ 100,2

Далее, с помощью формулы (2.15) найдем исправленную выборочную дисперсию и исправленное выборочное среднее квадратическое отклонение

А теперь рассмотрим нормально распределенную случайную величину K = - A0, экспериментальное (выборочное) значение которой при = 497,7 и A0 = 500 равно K = KЭксп = -2,3.

Если считать объем выборки N = 30 большим (хотя мы условились считать его большим лишь при N > 30), то область (-KКр; KКр) принятии гипотезы H0 можно найти, найдя KКр по формуле (3.4), в которой нужно заменить на . С учетом имеющихся данных находим:

KКр =

Итак, интервал принятия гипотезы H0 для значения случайной величины K = =- A0 Таков: - 3,7 < K < 3.7. Так как KЭксп = -2,3 принадлежит этому интервалу, то у нас нет оснований при заданном уровне значимости α = 0,05 отвергать нулевую гипотезу H0 о том, что автомат по разливу молока в пакеты настроен правильно.

Кстати, если величину α уменьшить, то интервал принятия гипотезы H0 расширится, а значит, будет еще больше оснований эту гипотезу не отвергать.

А теперь, для сравнения, проведем проверку гипотезы H0, считая объем N = 30 выборки небольшим, то есть используя формулы (3.5) и (3.6). Сначала найдем экспериментальное значение TЭксп. величины T:

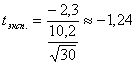
После этого по таблице 4 Приложения для α = 0,05 и K = N – 1 = 29 найдем критическое значение TКр распределения Стьюдента: TКр = 2,045. Таким образом, областью принятия гипотезы H0 является интервал

(- TКр ; TКр) = (-2,045; 2,045).

И так как TЭксп. = -1,24HHHHHHрРРваьйлуоатфыгу

содержится в этом интервале, то у нас нет оснований отвергать гипотезу H0­ о том, что автомат по разливу молока в пакеты настроен правильно.

< Предыдущая		Следующая >