1.30. Понятие о множественной корреляции
Случайная величина Y может корреляционно (в среднем) зависеть не от одной, а от нескольких случайных величин ![]() . Например, урожайность Y любой культуры очевидным образом корреляционно (в среднем) зависит от количества Х
. Например, урожайность Y любой культуры очевидным образом корреляционно (в среднем) зависит от количества Х![]() внесённых под неё удобрений, количества Х
внесённых под неё удобрений, количества Х![]() выпавших осадков, температуры Х
выпавших осадков, температуры Х![]() воздуха и т. д. Такая корреляционная зависимость называется Множественной корреляцией.
воздуха и т. д. Такая корреляционная зависимость называется Множественной корреляцией.
Пусть, например, случайная величина Z (дискретная или непрерывная) корреляционно зависит от некоторых двух случайных величин X и Y. Наличие такой корреляционной зависимости означает, что среднее значение ![]() величины Z, соответствующее значениям (X; Y) величин X и Y, зависит от этих (X; Y):
величины Z, соответствующее значениям (X; Y) величин X и Y, зависит от этих (X; Y):
![]() (6.47)
(6.47)
Уравнение (6.47) называется Уравнением регрессии Z на X и Y. В частности, если ![]() – линейная функция своих аргументов, то есть если
– линейная функция своих аргументов, то есть если
![]()
То корреляционная зависимость Z От X и Y называется Линейной. В противном случае она называется Нелинейной.
При исследовании множественной корреляционной зависимости, как и при исследовании парной (Y от X) корреляционной зависимости, ставятся те же две основные задачи:
1) Нахождение Уравнения регрессии, Выражающего зависимость среднего значения одной случайной величины от значений других случайных величин.
2) Оценка тесноты исследуемой корреляционной зависимости.
Исследование множественной корреляции – задача несравненно более сложная, чем исследование парной корреляции. При этом исследовании приходится выяснить наличие, характер и степень тесноты зависимости между каждой парой рассматриваемых случайных величин, находить некие коэффициенты их групповой взаимозависимости, и т. д. В практическом плане множественную корреляцию (впрочем, как и парную) исследуют в математической статистике – науке, которой посвящена вторая часть этой книги. Это исследование обычно производят с помощью специальных программ корреляционно – регрессионного анализа на ЭВМ.
Упражнения.
1. Доказать следующие свойства коэффициента линейной корреляции:
а)![]() б)
б)![]()
в)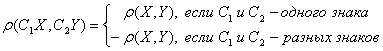
2. Выше было доказано, что если корреляционное отношение ![]() , то случайная величина Y корреляционно от Х не зависит. А если
, то случайная величина Y корреляционно от Х не зависит. А если ![]() , то Y является функцией от Х. Доказать, что верны и обратные этим утверждения.
, то Y является функцией от Х. Доказать, что верны и обратные этим утверждения.
3. Используя данные примера, приведённого в конце параграфа, выполнить его задания, поменяв Х и Y местами.
Ответ: 1)![]() 2)
2) ![]() 3) Линия регрессии
3) Линия регрессии ![]() - прямая, проходящая через две точки:
- прямая, проходящая через две точки:
|
|
0 |
1 |
|
|
1,1818 |
1,4286 |
| < Предыдущая | Следующая > |
|---|