1.29. Корреляционная зависимость случайных величин. Корреляционный момент (ковариация) и коэффициент линейной корреляции. Корреляционное отношение

Пусть X и Y – любые две случайные величины (дискретные или непрерывные – неважно). Нас будет интересовать связь между ними. Относительно этой связи имеется, в принципе, три возможности.

1) Первая возможность: величины X и Y независимы друг от друга. Это значит, что каждая из этих величин принимает свои значения независимо от значений, принимаемых другой случайной величиной.

2) Вторая возможность - обратная первой: величины Х и Y связаны жесткой (функциональной) зависимостью, т. е. зависимостью вида Y=. В этом случае каждому возможному значению величины Y соответствуют вполне определенное значение Y= величины Y. То есть возможные значения величины Y Жестко привязаны к возможным значениям величины X. Этому случаю был посвящен предыдущий параграф.

3) Третья возможность - промежуточная между первыми двумя: Х и Y в принципе связаны между собой (независимыми они не являются), но эта связь не жёсткая (размытая). Это значит, что каждому возможному значению Х величины Х могут соответствовать различные значения (У; у; ... ) величины Y, причём набор этих значений и (или) их вероятности меняются с изменением значения Х. Такого рода связь между случайными величинами называются Статистической (или Вероятностной) связью. Статистическая связь между случайными величинами X и Y означает, что изменение значения одной из них ведет к изменению Внешних условий Для реализации другой величины. Например, меняющаяся среднесуточная температура статистически влияет на плотность сельскохозяйственных вредителей на засеянном поле; объем денежной массы у покупателей статистически влияет на объем закупаемых ими товаров, и т. д.

Если при статистической связи между случайными величинами X и Y при изменении значения Х величины X еще и меняется Среднее значение величины Y, то говорят, что Y Корреляционно (в среднем) зависит от X. Аналогично понимается корреляционная зависимость X от Y. В частности, очевидно, что между температурой X воздуха и количеством Y вредителей имеет место не просто статистическая, а корреляционная зависимость, ибо с изменением температуры изменяется и среднее количество сельскохозяйственных вредителей. Аналогично между количеством X денег у покупателей и их тратами Y на покупку товаров тоже имеется, очевидно, корреляционная зависимость, ибо чем больше денег у покупателей, тем больше в среднем они покупают. Корреляционно (в среднем) связаны также урожайность различных культур с количеством внесенных под них удобрений, производительность труда рабочих с их квалификацией, и т. д.

Рассмотрим корреляционную связь между случайными величинами X и Y подробнее. Пусть - среднее значение тех значений У Величины Y, которые соответствуют данному значению X величины X. Оно же - условное математическое ожидание величины Y при X=X:

(6.1)

Так как каждому возможному значению X величины X будет соответствовать единственное значение , то это значение является функцией от X:

(6.2)

Если меняется с изменением X, то есть если , то между X и Y Имеется корреляционная связь – Y корреляционно (в среднем) зависит от X. А если , то Y корреляционно от X не зависит. В последнем случае Y либо вообще не зависит от X, либо зависит, но лишь сугубо статистически.

Функциональная зависимость (6.2) называется Уравнением регрессии Y на X, А график этой зависимости – Линией регрессии Y на X (рис 2.22):

Линия регрессии Y на X наглядно показывает, как В среднем меняется случайная величинаY при изменении случайной величины X. Точки вокруг линии регрессии символизируют разброс возможных значений Y величины Y вокруг линии регрессии . Именно из этих значений Y для каждого X Должно быть найдено их среднее значение .

Аналогично зависимость вида называется Уравнением регрессии X на Y, а ее график – Линией регрессии X на Y (рис 2.23).

Линия регрессии X на Y показывает, как В среднем меняется X при изменении Y.

Самой простой случай (и наиболее часто встречающийся на практике) – это когда функция или линейна, то есть когда её график – прямая линия. В этом случае корреляционная зависимость Y от X и соответственно корреляционная зависимость X от Y Называется Линейной, в противном случае – Нелинейной.

В теории корреляции решаются Две основные задачи:

Первая задача теории корреляции - нахождение Уравнения регрессии, то есть нахождение зависимости между значениями одной случайной величины и соответствующими им средними значениями другой случайной величины.

Вторая задача теории корреляции – оценка Тесноты изучаемой корреляционной зависимости. В частности, теснота корреляционной зависимости Y от Х оценивается по степени рассеяния значений (У; у; ....) величины Y (рис. 2.22) вокруг линии регрессии . Большое рассеяние свидетельствует о слабой корреляционной зависимости Y от Х. Наоборот, малое рассеяние указывает на наличие достаточно сильной (тесной) корреляционной зависимости. Возможно даже, что Y зависит от Х функционально, то есть жёстко, но из-за второстепенных случайных факторов или просто из-за погрешностей измерений эта зависимость оказалась несколько размытой.

Те же задачи, естественно, стоят, если исследуется корреляционная зависимость X от Y.

Наиболее просто решаются обе эти задачи при наличии линейной корреляционной зависимости одной случайной величины от другой. И здесь важную роль играет так называемый Корреляционный момент Или, что одно и то же, Ковариация случайных величин Х и Y, которые определяются как математическое ожидание произведения отклонений Х и Y От их математических ожиданий:

(6.4)

Их можно преобразовать к виду (проделайте это самостоятельно):

(6.5)

Как известно, у независимых случайных величин Х И Y, как у дискретных, так и у непрерывных, . А значит, для независимых случайных величин

(6.6)

Поэтому если , то это автоматически указывает на зависимость случайных величин Х и Y друг от друга.

Отметим, что обратное, вообще говоря, неверно: из того, что корреляционный момент , ещё нельзя сделать вывод, что Х И Y независимы. Они могут быть зависимы, причём даже функционально. Например, если распределение величины Х симметрично относительно точки Х=0,так что автоматически и , а - функция от Х, то на основании (6.5) получаем:

И это несмотря на то, что Х и Y связаны функциональной зависимостью

Случайные величины, для которых , называются Линейно некоррелированными. Независимые величины всегда линейно некоррелированы. Но линейно некоррелированные величины могут быть, как мы только что видели, как зависимыми, так и независимыми. Линейно коррелированные же величины (для них ) всегда зависимы.

Кстати, если случайные величины X И Y распределены нормально, то можно доказать (на этом не останавливаемся), что Их линейная некоррелированность равнозначна их независимости. Для других же величин Х и Y это не обязательно одно и тоже.

Отметим, что корреляционный момент обладает одним существенным недостатком: он зависит от единиц измерения величин X И Y. Поэтому на практике вместо него часто используется безразмерная величина

(6.7)

Которая называется Коэффициентом линейной корреляции. Он играет, как мы увидим ниже, большую роль при решении обеих задач теории корреляции в случае линейной корреляционной зависимости между случайными величинами.

Корреляционный момент и коэффициент линейной корреляции равны или не равны нулю одновременно. Поэтому линейную коррелированность и линейную некоррелированность случайных величин X и Y можно устанавливать и по равенству или неравенству нулю коэффициента линейной корреляции .

Так как, согласно (6.5), , то и

= (6.8)

Коэффициент линейной корреляции обладает еще одним важным свойством: он не изменится, если от X и Y перейти к безразмерным нормированным случайным величинам

(6.9)

То есть

= (6.10)

Нормированными случайными величинами и называются потому, что их математические ожидания равны нулю, а средние квадратические отклонения равны единице:

()= ()= (6.11)

Равенства (6.11) легко доказываются с помощью свойств (3.17) – (3.23) математического ожидания и дисперсии, которые справедливы как для непрерывных, так и для дискретных случайных величин (проделайте это самостоятельно). Ну, а то, что=, уже вытекает из (6.4), (6.5), (6.7), (6.9) и (6.11):

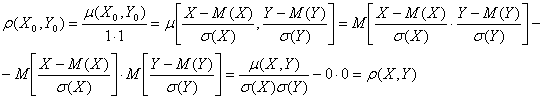
Для дальнейшего рассмотрения свойств коэффициента линейной корреляции случайных величин X и Y найдем дисперсию их суммы X+Y и разности X-Y. Если величина X и Y независимы, то такая формула уже получена (см. (3.22)):

(6.12)

Причем эта формула верна как для дискретных, так и для непрерывных случайных величин. А если X и Y зависимы (функционально или статистически), то соответствующая формула имеет вид:

(6.13)

Действительно:

В частности, для нормированных случайных величин формула (6.13) примет вид:

(6.14)

А так как, по смыслу дисперсии, , то из (6.14) получаем:

(6.15)

И так как, согласно (6.10), ) = , то для любых случайных величин Х и Y получаем следующий вывод:

(6,16)

Если коэффициент линейной корреляции , то он характеризует не только Наличие зависимости (связи) между Х и Y. Своей величиной, как мы это сейчас увидим, он характеризует И тесноту этой связи. Однако не любой, а Лишь линейной корреляционной связи между Х и Y. Отсюда и его название – коэффициент Линейной корреляции. Максимальная теснота этой связи соответствует случаям, когда = . При этом между Х и Y имеет место жёсткая функциональная связь, причём связь непременно линейная: .

Действительно, при = и )=, а тогда из (6.14) вытекает, что имеет место одно из двух равенств: или , или . Но дисперсия случайной величины равна нулю, если только эта случайная величина является константой. То есть или , или . Заметим, что в обоих случаях константа , ибо на основании (6.11) получаем:

Итак, при = либо , либо . А отсюда уже, согласно связи (6.9) с , следует подтверждение того, что в обоих случаях величины Х и Y связаны линейной функциональной зависимостью вида .

Верно и обратное: если случайные величины Х и Y связаны линейной функциональной зависимостью , то их коэффициент линейной корреляции Равен либо 1, либо -1.

Докажем это. Действительно, если , то согласно (6.9) и свойств математического ожидания и дисперсии получаем:

; =

=.

А тогда

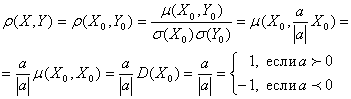
Таким образом, коэффициент линейной корреляции есть показатель того, насколько зависимость между случайными величинами X и Y близка к строгой линейной зависимости . Его малость (удаленность от может означать одно из двух: или малую тесноту (большое рассеяние) линейной корреляционной связи между X и Y, или существенную нелинейность этой связи, которая, кстати, может быть весьма тесной.

Сформулируем это утверждение более определенно. Найдем такие числовые коэффициенты K и B, чтобы линейная функция КX+B случайной величины X наилучшим образом приближала случайную величину Y. Для этого представим Y в виде

Y=кX+B+Z (6.17) Случайную величину Z можно рассматривать как ошибку приближения величины Y линейной функцией Y=кX+B. Эту ошибку естественно считать минимальной, если потребовать, чтобы математическое ожидание и дисперсия была минимальной. Первое из этих требований дает:

(6.18)

С учетом найденного значения B и (6.17) ошибка Z примет вид:

Теперь вычислим – дисперсию величины Z:

=

Первое из полученных слагаемых неотрицательно и не зависит от параметра K. Таким образом, дисперсия ошибки Z будет минимальной при том значении K, которое обеспечит обращение в нуль второго слагаемого. То есть при

(6.19)

При этом дисперсия (её минимальное значение) примет вид:

(6.20)

Итак, вывод: наилучшее приближение случайной величины Y линейной функцией КX+B случайной величины Х будет иметь место при значениях K и B, определяемых формулами (6.19) и (6.18). То есть такое приближение будет иметь вид:

(6.21)

Ошибка Z Этого линейного приближения величины Y имеет математическое ожидание (среднее значение), равное нулю. А дисперсия этой ошибки определяется формулой (6.20).

Если , то дисперсия ошибки . А это, с учетом равенства означает, что . То есть при в равенстве (6.21) ошибки нет и оно является точным. Но чем больше удален коэффициент линейной корреляции От , то есть чем ближе он к нулю, тем больше становится дисперсия ошибки Z, а вместе с ней тем больше становится и сама ошибка Z приближения (6.21). При Эта ошибка становится максимально возможной, а само приближение (6.21) принимает вид и перестаёт, таким образом, зависеть от X. То есть при =0 линейная зависимость Y от X отсутствует. Это значит, что или между случайными величинами X и Y вообще нет никакой связи, или они связаны, но какой-то нелинейной связью (функциональной или статистической).

Кстати, так как наилучшим приближением случайной величины Y при X=X является, очевидно, условная средняя , то из (6.21) сразу вытекает Наилучшее линейное приближение уравнения регрессии величины Y на величину X. Для его получения нужно в (6.21) заменить X На X и Y на . В итоге получим:

(6.22)

Здесь

(6.23)

Полученное простое линейное уравнение (6.22) используют на практике для приближенной замены истинного уравнения регрессии , если линия регрессии близка к прямой. Если же она сильно отличается от прямой (как на рис. 2.22), то его тоже можно использовать, только не на всем интервале (А; B) возможных значений величины X, а на коротких частях этого интервала, на которых линию регрессии можно приближенно считать прямой.

При приближенное линейное уравнение (6.22) становится точным. То есть становится истинным уравнением регрессии Y на X. Более того, при этом Превращается просто в Y – в единственное значение Y при X=X. Это происходит потому, что при становится точным равенство (6.21). А это значит, что каждому значению X величины X будет соответствовать единственное значение Y величины Y. И, таким образом, будет . Линия регрессии (см. рис. 2.22) станет прямой, и никакого разброса вокруг неё точек, изображающих возможные значения величины Y, не будет – все они окажутся на этой прямой.

Но если , то по мере удаления его значения от 1 истинная линия регрессии или искривляется, или остается прямой, но вокруг нее появляется облако точек, причем тем более широкое, чем ближе к нулю. Или одновременно и линия регрессии искривляется, и облако точек вокруг нее расширяется. При близком к нулю или тем более равном нулю нельзя даже приближено считать величины X И Y Связанными линейной корреляционной зависимостью. Связь между этими линейно некоррелированными (или слабо линейно коррелированными) случайными величинами будет или отсутствовать вообще, или будет существенно нелинейной. То есть в этом случае полученные выше формулы (6.21) и (6.22) приближенного линейного выражения одной величины (Y) через другую величину (Х) применять нельзя - они могут давать слишком грубое приближение. Тут требуется дополнительное исследование характера связи между такого рода слабо линейно коррелированными случайными величинами X и Y, которое мы проведем ниже.

Перейдем к этому исследованию. То есть поставим вопрос об оценке тесноты Любой, А не только линейной, корреляционной связи между случайными величинами X и Y.

Итак, допустим, что корреляционная связь между случайными величинами X и Y есть, и эта связь заведомо нелинейная (квадратичная, экспоненциальная, логарифмическая, и т. д.). Это значит, что уравнение Регрессии Y на Х таково, что и при этом . То есть линия регрессии Y На Х – кривая линия (рис. 2.22). Для оценки тесноты такой криволинейной корреляционной связи между X и Y коэффициент линейной корреляции , который будет близок к нулю, не годится. В этом случае указанною тесноту оценивают с помощью так называемого Корреляционного отношения.

Чтобы ввести это понятие, рассмотрим случайною величину , которая является функцией величины Х и которая при Х = х Принимает среднее значение величины Y. Математическое ожидание величины Совпадает с математическим ожиданием (средним значением ) величины Y:

(6.24)

А дисперсия Величины составляет лишь часть дисперсии величины Y:

(6.25)

При доказательстве равенств (6.24) и (6.25) ограничимся случаем, когда X и Y – дискретные случайные величины.

Итак, пусть X и Y – зависимые дискретные случайные величины, а таблица (6.26) – закон их совместного распределения:

X Y	Х	Х	............	Х	Q	(6.26)
Y	P	P	............	P	Q
Y	P	P	............	P	Q
.......	.......	.......	............	.......	.......
Y	P	P	............	P	Q
Pi	P	P	............	P	1

Здесь (X, X,… X) и (Y, Y,…Y) – возможные значения величин X и Y соответственно, а - вероятности того, что в результате испытания парой случайных величинБудет принята пара значений . Кстати, сумма всех вероятностей , как сумма вероятностей событий, составляющих полную группу событий, должна равняться единице:

(6.27)

Действительно, события, состоящие в том, что , являются несовместными. Причем одно из них обязательно произойдет. То есть эти события действительно образуют полную группу событий.

В последней строке таблицы (6.26) просуммированы вероятности по строкам (внутри каждого столбца). А в последнем столбце этой таблицы просуммированы вероятности по столбцам (внутри каждой строки):

(6.28)

Вероятности - это, очевидно, вероятности значений величины X, а вероятности - это вероятности значений величины Y. То есть на базе закона совместного распределения случайных величин X и Y можно записать и законы распределения каждой из этих величин в отдельности:

			…						…		(6.29)
			…					…

Среднее значение Величины Y для каждого возможного значения величины Y следует находить по формуле:

(6.30)

Действительно, согласно (6.1)

(6.31)

То есть - это условное математическое ожидание величины Y при X=. А следовательно, оно должно быть найдено как сумма произведений значений величины Y на соответствующее им вероятности этих значений при условии, что X=. То есть

(6.32)

А условные вероятности можно найти из формулы вероятности произведения двух зависимых событий (формула (4.5) главы 1):

(6.33)

Из формул (6.32) и (6.33) и следует формула (6.30).

Подсчитав значения , можем составить и закон распределения случайной величины :

			…		(6.34)
			…

(вероятности значений величины те же, что и вероятности значений величины X).

Ну, а теперь можем перейти к доказательству равенств (6.24) и (6.25). Сначала докажем (6.24):

(6.35)

Равенство (6.24) доказано.

Для доказательства равенства (6.25) образует случайную величину и запишем закон её распределения:

		(6.36)

Математическое ожидание этой случайной величины равно нулю - это следует из (6.24). Покажем ещё, что

(6.37)

Закон распределения случайной величины Имеет вид:

		(6.38)

Отсюда следует:

=

= = . (6.39)

А теперь, опираясь на доказанные равенства (6.24) и (6.37), можно доказать и равенство (6.25):

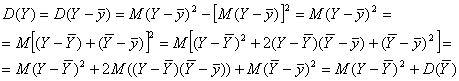
Равенство (6.25) доказано. Это равенство дает разложение общей дисперсии зависимой от X случайной величины Y на сумму двух слагаемых: дисперсии функции и среднего квадрата отклонения Y от этой функции. Иначе говоря, общий разброс значений У Величины Y Вокруг её среднего значения складывается из разброса значений величины вокруг того же , и разброса значений У вокруг . То есть формула (6.25) раскладывает общий разброс всех возможных значений Y Величины Y вокруг её математического ожидания на разброс вокруг точек Кривой регрессии, и на разброс значений У (облака точек, изображающих значения Y) вокруг кривой регрессии

Введем теперь отношение

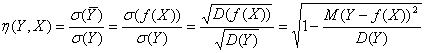(6.40)

Которое будет называть Корреляционным отношением Y к X. Очевидно, что всегда

(6.41)

Из определения следует, что =0 при , то есть при условии, что =Const. Причем эта константа, естественно, равна . Но тогда уравнение регрессии Y на X имеет вид = и, следовательно, случайная величина Y не зависит корреляционно (в среднем) от величины X. А если , то в этом случае из (6.40) следует, что =0, откуда вытекает, что . То есть при случайные величины X и Y связаны жесткой функциональной зависимостью , причем Const.

Из сказанного следует, что чем ближе корреляционное отношение к единице, тем ближе корреляционная зависимость Y от X к функциональной зависимости. А это значит, тем эта корреляционная зависимость теснее. Наоборот, чем ближе к нулю, тем она слабее.

Таким образом, корреляционное отношение случайной величины Y К случайной величине X является мерой и наличия, и тесноты Любой (а не только линейной) корреляционной зависимости величины Y от величины X.

Естественно, можно ввести в рассмотрение и корреляционное отношение величины X к величине Y.

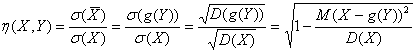(6.42)

Которое оценивает наличие и тесноту корреляционной зависимости величины X от Y, где - уравнение регрессии X на Y.

Отметим, что в отличие от коэффициента линейной корреляции, которой симметричен относительно X и Y (), корреляционное отношение таким свойством, судя по (6.40) и (6.42), не обладает:

(6.43)

Можно еще доказать, что всегда

(6.44)

При этом в случае равенства

(6.45)

Имеет место Точная линейная корреляционная зависимость Y от X. Это значит, что при условии (6.45) приближенное уравнение регрессии (6.22) Y на X становится Точным.

Аналогично в случае

(6.46)

Становится точным соответствующее уравнение регрессии X на Y.

Пример. Дискретные случайные величины X и Y заданы следующим законом их совместного распределения:

X Y	0	1	2
0	0,10	0,16	0,18	0,44
1	0,06	0,20	0,30	0,56
	0,16	0,36	0,48	1

Требуется:

1) Найти коэффициент линейной корреляции .

2) Найти корреляционное отношение .

3) Построить линию регрессии величины Y на величину X.

Решение. Запишем сначала законы распределения величин X и Y по отдельности:

X	0	1	2		Y	0	1
Р	0,16	0,36	0,48	Р	0,44	0,56

Отсюда, в частности, следует (получите это самостоятельно):

;

Теперь найдем . Для этого, согласно (6.7), предварительно нужно найти корреляционный момент . Его найдем по формуле (6.5), используя совместный закон распределения (таблицу) величины Х и Y:

Тогда:

Величина . Таким образом, величины X и Y линейно коррелированы, а значит и зависимы. Вместе с тем величина Невелика (она гораздо ближе к нулю, чем к 1 или к -1). Поэтому корреляционная зависимость Y от Х или слабая, или существенно нелинейная, или то и другое вместе.

Чтобы лучше выяснить этот вопрос, подсчитаем корреляционное отношение величины Y к величине Х. Для этого сначала для каждого значения Х величины Х подсчитаем среднее значение величины Y. Используя формулы (6.30), получим:

Полученные данные позволяют записать таблицу вида (6.34) - закон распределения функции Случайной величины Х:

	0,375	0,556	0,625
Р	0,16	0,36	0,48

Из этой таблицы находим:

=.

Величина оказалась большей, чем - так и должно, согласно (6.44), быть. Однако и она невелика, что свидетельствует о малой тесноте корреляционной зависимости Y и X. А так как различие между и Незначительное, то корреляционная зависимость Y от X близка к линейной.

Этот вывод должна подтвердить линия регрессии . Ее следует строить по трем точкам:

	0	1	2
	0,375	0,556	0,625

Как легко убедиться, ломаная, соединяющая эти три точки, действительна близка к прямой линии.

< Предыдущая		Следующая >