1.28. Функция случайной величины

Пусть Y – случайная величина, значение которой полностью определяется значением другой случайной величины X. То есть случайная величина Y является Функцией случайной величины X:

(5.1)

Например, если изготавливаются цилиндрические болванки, и X – диаметр болванок (X – случайная величина), то

(5.2)

- площадь поперечного сечения этих болванок, которая тоже является случайной величиной. И эта величина Y – функция величины X. Аналогично доход Y=PX от ежедневных продаж товара – функция от объема X проданного товара, где Р – цена единицы товара. И т. д.

Пусть известно распределение случайной величины X (аргумента). Спрашивается, каким будет распределение случайной величины - функции величины X? Ответ на этот вопрос, очевидно, должен быть отдельным для дискретных и отдельным для непрерывных случайных величин.

1. Пусть X – дискретная случайная величина, а таблица (5.3) – закон ее распределения:

Х			…		(5.3)
Р			…

Тогда - тоже дискретная случайная величина, а таблица (5.4) – закон её распределения:

			…		(5.4)
Р			…

Действительно, значениями случайной величины Будут значения …, а вероятности Р; р;...р у этих значений будут теми же, что и у значений х; х;...х. Последние обстоятельство следует из того факта, что события Х= хИ ) (I=1,2,…N) наступают или не наступают одновременно. Значит, они имеют одинаковые вероятности.

Пример 1. Случайная величина Х имеет следующий закон распределения:

Х	-1	0	1	2
Р	0.5	0.2	0.2	0.1

Составить закон распределения случайной величины Y=Х.

Решение. Согласно (5.4) имеем:

	1	0	1	4
Р	0.5	0.2	0.2	0.1

Суммируя вероятности совпадающих значений, получим окончательно:

	0	1	4
Р	0.2	0.7	0.1

После того, как закон распределения функции составлен, можно, при желании, найти и её числовые характеристики М(Y), D(Y), S(Y) , V(Y).

2. Пусть теперь Х - непрерывная случайная величина, распределение которой задаётся интервалом (A; B) её возможных значений и плотностью вероятности F (х) для Х (A;B). Тогда - тоже непрерывная случайная величина. Распределение величины Y будет известно, если мы найдём интервал (С; D) её возможных значений У и плотность вероятности G(у) для У (С; D).

Сразу отметим, что интервал (С ; D), который содержит все возможные значения У случайной величины , представляет собой, очевидно, область значений функции У=(а<х<B). А плотность вероятности G(у) величины Будем искать, исходя из следующих соображений.

Пусть Х - некоторое возможное значение величины Х (А<х<B). Тогда Y= (C<Y<D) – соответствующее ему значение величины Y. Окружим точку X некоторым бесконечно малым отрезком длиной Dx. Тогда этому отрезку, окружающему точку X, будет соответствовать некоторой бесконечно малый отрезок длиной , окружающий точку Y (рис. 2.21)

В выражении производная взята по модулю с тем, чтобы выражение для длины Dy было верным и для возрастающей функции (когда ), и для убывающей (когда ).

Попадание значения случайной величины X на отрезок Dx будет, очевидно, автоматически означать попадание значения случайной величины Y на отрезок Dy. Вероятности Dp появления обоих этих событий, таким образом, одинаковы. Следовательно, одновременно имеем:

(5.5)

Сравнивая эти два значения Dp, получаем:

(5.6)

Чтобы получить окончательное выражение для G (у), нужно правую часть равенства (5.6) выразить через У. Для этого из равенства У =, связывающего Х и У, нужно Х выразить через У. То есть нужно найти функцию Х = , обратную к функции У = . Такая обратная функция заведомо существует, если исходная функция У = Монотонно возрастает или монотонно убывает, что мы и будем предполагать. Найдя функцию X = , можем и производную функции У =Выразить через Y:

= (5.7)

С учетом этого функция G(Y) причем следующий окончательный вид:

(C<Y<D) (5.8)

Это и есть плотность вероятности непрерывной случайной величины Y, являющейся функцией Y=Непрерывной случайной величины Х. При этом - плотность вероятности величины Х, а X = - функция, обратная функции У= = .

После того, как найдена плотность вероятности Случайной величины , можно, при желании, найти все числовые характеристики этой величины:

; , где 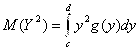; (5.9)

Впрочем, для нахождения этих числовых характеристик величины не обязательно находить функцию G(Y). Подставляя в интегралы (5.9) выражение (5.8) для G(Y) и делая затем подстановку X = , получим (выкладки проделайте самостоятельно):

;

; (5.10)

;

Пример 2. Непрерывная случайная величина Х задана плотностью вероятности (0). Найти плотность вероятности случайной величины Y = , а также вычислить её основные числовые характеристики.

Решение. Сначала найдём промежуток Возможных значений У величины Y=. То есть найдем область значений функции У = (0). Она очевидна: 0. То есть = .

Теперь найдём G( у ) (0) – плотность вероятности случайной величины Y . Так как У = (0) , то Х = ( 0 ), а . И тогда, согласно (5.8), получаем :

(0) (5.11)

А отсюда уже, согласно (5.9), находим:

; ;

; ;

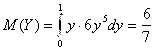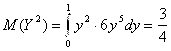Впрочем, для нахождения числовых характеристик случайной величины Y= можно было бы применить и формулы (5.10):

;

;

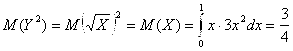Пример 3. Непрерывная случайная величина X распределена нормально с параметрами (; ). Доказать, что любая линейная функция Y= ( этой величины X тоже распределена нормально с параметрами (; ).

Доказательство. Плотность вероятности нормально распределенной величины X имеет, как известно, вид:

(-

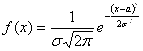Так как возможные значения X величины X - любые числа от - до , то и возможные значения У величины Y=- любые числа. То есть интервал (C; D) возможных значений величины Y – это вся ось Oy От - до .

Теперь найдем G(Y) (-<x< ) - плотность вероятности случайной величины Y. Так как Y=, то X = , а . И тогда, согласно (5.8), получаем

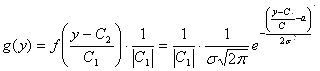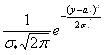= (- <Y< ),

Где

.

Доказательство закончено.

Для нормально распределенных случайных величин доказан и более общий факт: если (X; X;…;X) – независимые нормально распределенные случайные величины, то любая их линейная комбинация

Z= X+C…+CX (5.12)

Тоже является случайной величиной, распределенной нормально. И если () – параметры величин X (K = 1, 2,..., P), то параметры () величины Z Таковы:

(5.13)

Упражнения

1. Дискретная случайная величина X Задана законом распределения

X	-1	-2	1	2
P	0.3	0.1	0.2	0.4

Найти закон распределения величины и ее числовые характеристики.

Ответ:

Y	1	2
P	0.5	0.5

2. Случайная величина X Распределена равномерно. Доказать, что любая линейная функция () величины X тоже распределена равномерно.

3. Случайная величина X распределена по показательному закону. Доказать, что линейная функция величины X тоже будет распределена по показательному закону, но лишь при >0 и =0.

4. Случайная величина X распределена нормально с параметрами (). Доказать, что случайная величина тоже будет распределена нормально с параметрами то есть будет нормированный нормально распределенной случайной величиной.

< Предыдущая		Следующая >