1.27. Показательное распределение. Функция надежности
Пусть некоторый природный или искусственный объект начинает функционировать в момент времени T=0. В качестве такого объекта можно, например, рассматривать живое существо с момента его рождения или с любого другого этапного для него момента; работающий механизм или элемент этого механизма с момента его включения, и т. д.
Пусть Т – время безаварийного функционирования этого объекта (для живого существа это может быть время до утраты пригодности его к тому или иному виду деятельности или до его смерти; для механизма это может быть время до первой его поломки или до окончательного выхода его из строя, и т. д.). Согласно своего смысла, Т – непрерывная случайная величина, возможные значения T которой могут быть, в принципе, любыми неотрицательными числами: ![]() .
.
Поставим теперь естественный вопрос: какова вероятность ![]() того, что для данного объекта будет иметь место неравенство
того, что для данного объекта будет иметь место неравенство ![]() , где T – некоторое заданное время? То есть поставим вопрос: какова вероятность того, что за время T функционирующий объект не выйдет из строя? Вероятность эту обозначим символом R(T) и назовем Функцией надежности:
, где T – некоторое заданное время? То есть поставим вопрос: какова вероятность того, что за время T функционирующий объект не выйдет из строя? Вероятность эту обозначим символом R(T) и назовем Функцией надежности:
![]()
![]() (4.22)
(4.22)
Очевидно, что для любого функционирующего объекта указанная вероятность R(T) сохранения своей работоспособности в течение времени T будет убывать с возрастанием T, Начиная с 1 при T=0, и стремиться к нулю при ![]() . Более того, как показали многочисленные практические исследования самых разнообразных объектов (технических устройств; природных образований; живых организмов и т. д.) это убывание функции надежности R(T) осуществляется приблизительно по показательному (экспоненциальному) закону
. Более того, как показали многочисленные практические исследования самых разнообразных объектов (технических устройств; природных образований; живых организмов и т. д.) это убывание функции надежности R(T) осуществляется приблизительно по показательному (экспоненциальному) закону
![]()
![]() (4.23)
(4.23)
 Такое поведение функции надежности R(T) называют еще Показательным законом надежности (рис.2.16).
Такое поведение функции надежности R(T) называют еще Показательным законом надежности (рис.2.16).
Выясним смысл параметра ![]() в случае показательного закона надежности. Для этого найдем плотность вероятности
в случае показательного закона надежности. Для этого найдем плотность вероятности ![]() и основные числовые характеристики (
и основные числовые характеристики (![]() ) случайной величины Т.
) случайной величины Т.
Начнем с нахождения ![]() . Ее будем искать, исходя из определения (3.1) плотности вероятности непрерывной случайной величины.
. Ее будем искать, исходя из определения (3.1) плотности вероятности непрерывной случайной величины.
Пусть T – некоторое фиксированное значение величины Т (T – момент выхода объекта из строя). Окружим это значение некоторым частичным промежутком [![]() ] длиной
] длиной ![]() и рассмотрим вероятность
и рассмотрим вероятность ![]() того, что случайная величина Т примет значение внутри этого промежутка. То есть рассмотрим вероятность
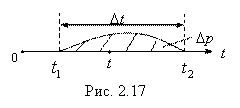
того, что случайная величина Т примет значение внутри этого промежутка. То есть рассмотрим вероятность ![]() того, что объект выйдет из строя в какой-то момент времени, принадлежащий этому промежутку (рис.2.17).
того, что объект выйдет из строя в какой-то момент времени, принадлежащий этому промежутку (рис.2.17).
|
|
|
![]() (4.24)
(4.24)
Тогда по формуле (3.1) получаем:
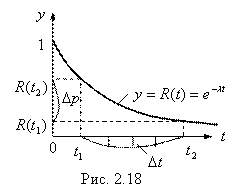 |
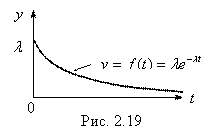

Итак,
![]() (4.25)
(4.25)
– плотность вероятности случайной величины Т, представляющей собой время безаварийного функционирования объекта, имеющего показательный закон надежности. График этой плотности вероятности изображен на рис.2.19. Кстати, распределение указанной случайной величины Т носит название Показательного распределения.
Зная плотность вероятности ![]() , можем теперь по формулам (3.9)-(3.14) найти и числовые характеристики (
, можем теперь по формулам (3.9)-(3.14) найти и числовые характеристики (![]() ) случайной величины Т (получите их самостоятельно):
) случайной величины Т (получите их самостоятельно):
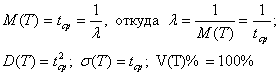 (4.26)
(4.26)
Здесь TСр – Среднее время безаварийного функционирования объекта. Через TСр можно выразить и функцию надежности (4.23) случайной величины Т, и плотность ее вероятности (4.25):
 (4.27)
(4.27)
В заключение отметим следующий важный факт: вероятность безаварийной работы любого объекта на интервале времени длительности T, если время Т безаварийной работы этого объекта имеет показательное распределение, Не зависит от начала рассматриваемого интервала, а зависит только от его длительности T.
Для доказательства этого утверждения введем следующие события (рис. 2.20):
 А – безотказное функционирование объекта на интервале времени (
А – безотказное функционирование объекта на интервале времени (![]() );
);
В – безотказное функционирование объекта на интервале времени (![]() );
);
С – безотказное функционирование объекта на интервале времени (![]() ):
):
Очевидно, что С=АВ, откуда следует:
![]() (4.28)
(4.28)
Таким образом
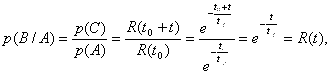 (4.29)
(4.29)
Где R(T) – вероятность безотказного функционирования объекта на интервале времени (![]() ), а
), а ![]() – вероятность безотказного функционирования объекта на интервале времени (
– вероятность безотказного функционирования объекта на интервале времени (![]() ). Эти вероятности равны, что и доказывает заявленный выше факт.
). Эти вероятности равны, что и доказывает заявленный выше факт.
Отметим, что случайные величины, имеющие показательное распределение (показательный закон надежности), тесно связаны с событиями простейшего (пуассоновского) потока. Действительно, согласно формуле (2.8) главы 1 вероятность того, что за время T не появится ни одного из событий простейшего потока, найдется по формуле:
![]() (4.30)
(4.30)
Здесь ![]() - интенсивность пуассоновского потока (среднее число событий потока, появляющихся за единицу времени). Тогда
- интенсивность пуассоновского потока (среднее число событий потока, появляющихся за единицу времени). Тогда ![]() – среднее время, проходящее между появлениями отдельных событий потока. С учетом этого вероятность (4.30) примет вид:
– среднее время, проходящее между появлениями отдельных событий потока. С учетом этого вероятность (4.30) примет вид:
![]() (4.31)
(4.31)
Но точно такой же вид, согласно (4.27), имеет показательная функция надежности R(T), определяющая вероятность безаварийной работы объекта в течение времени T. Таким образом, время Т безаварийной работы объекта при показательном законе надежности и время Т, проходящее между соседними событиями простейшего потока, имеют одно и то же распределение. А именно, показательное распределение с плотностью вероятности ![]() , описываемой формулой (4.27).
, описываемой формулой (4.27).
Пример 3. Среднее время безотказной работы некоторого устройства, имеющего показательный закон надежности, равно 50 часам. Определить вероятность того, что устройство безотказно проработает 100 часов.
Решение. Пусть Т – время безотказной работы устройства. Так как среднее значение этого времени TСр=50 часам, то функция надежности R(T) для рассматриваемого устройства имеет, согласно (4.27), вид:
![]() (T – В часах, T≥0)
(T – В часах, T≥0)
Тогда, согласно (4.22), получаем искомую вероятность:
![]()
Упражнения.
1. Интервал движения троллейбусов составляет 5 минут. Какова вероятность того, что пришедшему на остановку пассажиру придется ожидать очередного троллейбуса не менее трех минут?
Ответ: 0,4.
2. Производится взвешивание некоторого вещества без систематических ошибок со средней случайной ошибкой 20 г ( в ту или другую сторону). Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 г.
Ответ: 2Ф(0,5)≈0,383.
3. Норма высева семян на 1 га равна 200 кг. Фактический расход семян на 1 га колеблется около этого значения со средним квадратическим отклонением 10 кг. Определить количество семян, обеспечивающих посев на площади 100 га с гарантией (вероятностью) 0,95.
Ответ: 21645 кг.
4. Станок-автомат производит цилиндрические болванки. Проектный размер диаметра болванок составляет 100 мм. Известно, что станок производит в среднем 2 % болванок диаметром более 101 мм. Болванка считается годной, если ее диаметр находится в пределах от 99 мм до 101 мм. Сколько процентов годных болванок производит станок-автомат?
Ответ: 96%.
5. Испытывают два независимо работающих устройства. Длительность безотказной работы обоих устройств имеет показательное распределение. Среднее время безотказной работы первого устройства составляет 40 часов, второго 20 часов. Найти вероятность того, что в течение 10 часов:
А) не откажет первое устройство;
Б) не откажет второе устройство;
В) оба устройства не откажут;
Г) оба устройства откажут;
Д) хотя бы одно устройство не откажет.
Ответ: а) 0,78; б) 0,61; в) 0,47; г) 0,09; д) 0,91.
6. В городе рождается в среднем 5 детей в сутки. Считая рождения детей событиями, составляющими простейший поток событий, найти:
А) математическое ожидание;
Б) среднее квадратическое отклонение;
В) коэффициент вариации случайной величины Т – времени между последовательными рождениями детей.
Ответ: а) M(T)=4ч. 48мин.; б) S(Т)=4ч. 48мин.; в) V(T)%=100%.
| < Предыдущая | Следующая > |
|---|