1.31. Закон больших чисел

Закон больших чисел является центральным законом теории вероятностей в силу того, что он формулирует принципиальную связь между закономерностью и случайностью. А именно, он утверждает, что большое число случайностей ведет к закономерности. В наиболее общей форме он выражается Теоремой Чебышева:

Пусть (Χ1; X2; … Xn; …) независимые случайные величины (их, предполагается, бесконечное число). И пусть их дисперсии равномерно ограничены (то есть дисперсии всех этих случайных величин не превосходят некоторой константы С):

(7.1)

Тогда как бы ни было мало положительное число , выполняется предельное вероятностное соотношение:

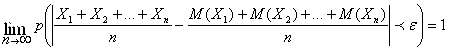(7.2)

Или, что одно и то же, вероятность

(7.3)

Таким образом, теорема Чебышева утверждает, что если рассматривать достаточное большое число N независимых случайных величин (Χ1; X2; … Xn), То почти достоверным (с вероятностью, близкой к единице) можно считать событие, состоящее в том, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Доказательство. Введем в рассмотрение новую случайную величину - среднее арифметическое случайных величин (Χ1; X2; … Xn):

(7.4)

Пользуясь свойствами математического ожидания и дисперсии, для получим:

; (7.5)

Учитывая условия (7.1), устанавливаем, что

(7.6)

Таким образом, при дисперсия . То есть при разброс значений случайной величины вокруг её математического ожидания неограниченно уменьшается. А это значит, что при величина, то есть . Или, если сказать точнее, к нулю стремиться вероятность того, что случайная величина будет хоть как-то отклоняться от своего математического ожидания – константы . А именно, при любом сколь угодно малом положительном числе

(7.7)

Итак, согласно доказанной теореме Чебышева, среднее арифметическое большого числа независимых случайных величин (Χ1; X2; … Xn), являясь случайной величиной, фактически утрачивает характер случайности, становясь, по сути, неизменной константой . Эта константа равна среднему арифметическому математических ожиданий величин (Χ1; X2; … Xn). В этом и состоит закон больших чисел.

Остановимся на одном важном частном случае теоремы Чебышева. А именно, рассмотрим случай, когда независимые случайные величины (Χ1; X2; … Xn) имеют одинаковые законы распределения, а, следовательно, и одинаковые числовые характеристики:

(7.8)

Тогда для случайной величины , согласно (7.5), имеем:

(7.9)

Предельное вероятностное соотношение (7.7) в этом случае примет вид:

(7.10)

Вывод, следующий из (7.10), имеет большое значение для борьбы со случайными ошибками при производстве различного рода измерений.

Пусть, например, требуется измерить некоторую величину А. Произведем не одно, а несколько (N) независимых повторных измерений значения этой величины. Любым измерениям присуща случайная ошибка, связанная с несовершенством измерительного прибора, всевозможными случайными помехами измерению, и т. д. Поэтому результаты (Χ1; X2; … Xn) отдельных последовательных измерений искомого значения А, вообще говоря, давать не будут - они будут случайными величинами. Причем величинами, имеющими одинаковые распределения, ибо измерения производятся повторно, то есть при неизменных внешних условиях. Тогда для величины - среднего арифметического из результатов всех N измерений - будет выполняться предельное вероятностное соотношение (7.10). А значит, это среднее арифметическое при утрачивает характер случайности, превращаясь в А – истинное значение измеряемой величины. Об этом, кстати, свидетельствуют и формулы (7.9), согласно которым:

(7.11)

То есть проведя достаточно большое число повторных измерений искомой величины А, в каждом из которых возможна случайная ошибка измерения, и находя затем среднее арифметическое результатов этих измерений, мы по формуле

а (7.12)

Можем получить значение А Практически без случайной ошибки.

Этот вывод - следствие закона больших чисел. В данном случае этот закон проявляется в том, что при суммировании результатов измерений в (7.4) случайные ошибки отдельных измерений, встречающиеся в принципе одинаково часто как со знаком плюс, так и со знаком минус, в целом будут взаимно уничтожаться. А оставшаяся ошибка еще разделится на П, то есть еще уменьшится в П раз. Так что при больших значениях N величина будет практически точно равна измеряемой величине А. Этим выводом, естественно, широко пользуются на практике.

Примечание. В величине взаимно уничтожаются лишь случайные ошибки измерений, то есть ошибки, связанные с действием случайных факторов (помех). Но систематические (постоянно действующие) ошибки, то есть ошибки, присущие каждому измерению, естественно, остаются и в . Например, сбитая (не отрегулированная) в приборе стрелка вызывает постоянную (систематическую) ошибку в каждом измерении, а значит вызывает её и в средней арифметической из результатов этих измерений. Систематические ошибки надо исключать еще до производства измерений и не допускать в процессе измерений.

Потом, если α – цена деления измерительного прибора, то все повторные измерения производятся с точностью до α. Но тогда, естественно, и среднее арифметическое из результатов всех измерений можно указывать лишь тоже с точностью до α, то есть с точностью, определяемой точностью прибора.

Поэтому не стоит думать, что сделав достаточно большое число повторных измерений величины А и найдя затем среднее арифметическое из результатов этих измерений, мы получим Точное Значение А. Мы его получим лишь в пределах точности измерительного прибора. Да и то, если исключим систематическую ошибку измерения.

Приведем еще один важный частный случай закона больших чисел. Пусть Х=K – число появлений некоторого события А в П повторных испытаниях (X – случайная величина). И пусть и – вероятности появления и непоявления события А в одном испытании. Рассмотрим случайную величину - относительную частоту появления события А в П Испытаниях. Введем также N случайных величин (Х1, Х2,…Xn), которые представляют собой число появление события А в первом, втором, … П-ом испытаниях. Тогда K = Х1+Х2+…+Хп , а

(7.13)

Случайные величины (Х1, Х2,…Xn) имеют одинаковые и простые законы распределения:

			(7.14)

Из (7.14) находим:

(7.15)

Предельное вероятностное соотношение (7.10) для рассматриваемого случая примет вид:

(7.16)

То есть при достаточно большом числе П повторных испытаний можно почти наверняка (с вероятностью, близкой к единице) ожидать, что относительная частота появления события А Практически совпадет с вероятностью появления события А В одном испытании. На этом выводе основано нахождение вероятностей многих случайных событий, чьи вероятности каким-то другим путем (теоретически) найти не удается.

Например, пусть испытание – это подбрасывание деформированной (несимметричной) монеты, а событие А для этого испытания – это выпадение герба. Вероятность события А по классической формуле или по какой-то другой теоретической формуле найти затруднительно, ибо в такой формуле должны быть как-то отражены характеристики деформации монеты. Поэтому реальный путь, ведущий к цели, здесь один: повторно бросать монету (чем больше число бросаний N, тем лучше) и определять опытным путем относительную частоту появления герба. Если N Велико, то в соответствии с законом больших чисел можно с большой вероятностью утверждать, что .

Закон больших чисел проявляет себя во многих природных и общественных явлениях.

Пример 1. Как известно, газ, помещенный в закрытый сосуд, оказывает давление на стенки сосуда. Согласно законам газового состояния, при неизменной температуре газа это давление постоянно. Давление газа имеет своей причиной хаотические удары отдельных его молекул о стенки сосуда. Скорости и направления движения у всех молекул разные, поэтому разными являются и силы ударов различных молекул о стенки сосуда. Однако давление газа на стенки сосуда определяется не силой ударов отдельных молекул, а их Средней силой. Но она, как средняя из огромного числа независимо действующих сил, согласно закону больших чисел, будет сохранять практически неизменное значение. Поэтому практически неизменным оказывается и давление газа на стенки сосуда.

Пример 2. Страховая компания, занимающаяся, например, автострахованием, выплачивает по разным страховым случаям (автомобильным авариям и ДТП) разные страховые суммы. Однако величина среднего значения этой страховой суммы, как среднего значения из многих различных N независимых страховых сумм, согласно закону больших чисел, будет практически неизменной. Ее можно определить, исследовав реальную статистику страховых случаев. Чтобы страховой компании не оказаться в убытке, средний размер страхового взноса, взимаемого с клиентов этой компании, должен быть выше средней страховой суммы, которую выплачивает компания своим клиентам. Но этот взнос не должен быть и слишком высоким, чтобы компания была конкурентноспособна (могла конкурировать по привлекательности с другими страховыми компаниями).

Упражнения

1. К какому типу случайных величин применим закон больших чисел: дискретным? непрерывным? зависимым? независимым? любым?

2. В некотором эксперименте требуется определить (измерить) некоторую величину. Как исключить возможную случайную ошибку измерения?

3. Непрерывная случайная величина X задана плотностью вероятности

(распределение Коши). Показать, что для средней арифметической из независимых случайных величин (Х1, Х2,…Xn, …), имеющих распределение Коши, неприменим закон больших чисел. То есть средняя при не стремится по вероятности ни к какому конечному числу.

< Предыдущая		Следующая >