1.24. Распределение (хи-квадрат)

Пусть – независимые нормированные нормально распределенные случайные величины (то есть у каждой из них = 0 и ). Тогда сумма квадратов этих величин

(4.13)

Является случайной величиной, распределенной По закону (хи-квадрат) с степенями свободы. Понятие «число степеней свободы» заимствовано из физики, где под ним понимается число независимых координат, определяющих положение тел в процессе их движения. В частности, при движении по прямой точка обладает одной степенью свободы; при свободном движении по плоскости – двумя степенями свободы; при свободном движении в пространстве – тремя степенями свободы. Если же движение точки несвободно – например, она может двигаться по плоскости лишь вдоль какой-то линии с уравнением , то ее положение на плоскости полностью определяется лишь одной координатой Х, ибо другая координата Y уже не является независимой, так как выражается через Х. В этом случае у движущейся по плоскости точки будет не две, а одна степень свободы. И так далее. Возвращаясь к выражению (4.13) для случайной величины , видим, что в ее образовании участвуют независимых величин . Поэтому у нее и степеней свободы.

Очевидно, что величина может принимать лишь неотрицательные значения . Доказано, что плотность вероятности случайной величины с степенями свободы имеет вид

(4.14)

Где - быстро убывающие с номером числовые коэффициенты, выражения которых ввиду их сложности не приводим. При этом график плотности вероятности для =1, =2 и >2 в принципе имеет вид:

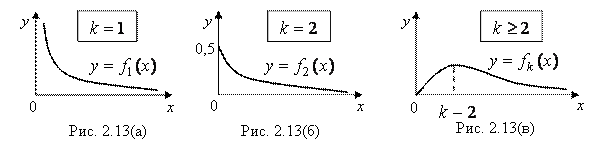
Также доказано, что

(4.15)

С увеличением числа Степеней свободы распределение медленно приближается к нормальному.

< Предыдущая		Следующая >