1.23. Нормальное распределение
Пусть случайная величина Х может быть представлена в виде:
![]() (4.5)
(4.5)
Здесь ![]() - некоторая константа, а
- некоторая константа, а ![]() - сумма очень большого (бесконечно большого) числа независимых случайных величин Хк, влияние каждой из которых на всю эту сумму ничтожно мало.
- сумма очень большого (бесконечно большого) числа независимых случайных величин Хк, влияние каждой из которых на всю эту сумму ничтожно мало.
Примерно такая ситуация, в частности, сложится, если Х – результат измерения некоторым прибором некоторой величины ![]() (например, Х – результат взвешивания на весах некоторой массы
(например, Х – результат взвешивания на весах некоторой массы ![]() ). Действительно, результат Х Измерения не обязательно совпадет с истинным значением
). Действительно, результат Х Измерения не обязательно совпадет с истинным значением ![]() измеряемой величины, ибо к этому истинному значению добавляются ошибки ХK, вносимые:
измеряемой величины, ибо к этому истинному значению добавляются ошибки ХK, вносимые:
А) прибором; б) измерителем; в) внешней средой.
Такого рода помех измерению в принципе бесконечно много, и каждая из них вносит свою ошибку ХK в результат Х измерения.
Если бы ошибок ХK не было (а значит, не было бы помех измерению), то результат измерения Х совпал бы с ![]() - с истинным значением измеряемой величины. И, таким образом, он не был бы случайной величиной. Но от окружающей среды защититься полностью невозможно. А потому ошибки ХK измерения, вызываемые помехами, неизбежны при любом измерении. Все эти ошибки ХK, вообще говоря, мелкие. Но их очень много, ибо очень много внешних факторов, влияющих на процесс измерения. Действуют эти факторы, как правило, независимо друг от друга. Поэтому результат Х измерения –случайная величина, которая в итоге и принимает вид (4.5).
- с истинным значением измеряемой величины. И, таким образом, он не был бы случайной величиной. Но от окружающей среды защититься полностью невозможно. А потому ошибки ХK измерения, вызываемые помехами, неизбежны при любом измерении. Все эти ошибки ХK, вообще говоря, мелкие. Но их очень много, ибо очень много внешних факторов, влияющих на процесс измерения. Действуют эти факторы, как правило, независимо друг от друга. Поэтому результат Х измерения –случайная величина, которая в итоге и принимает вид (4.5).
 Будем считать, что среди ошибок измерения нет ошибок систематических. То есть нет ошибок, приводящих к систематическому завышению или занижению результатов измерения (из-за неотрегулированности прибора, недобросовестности измерителя, и т. д.). То есть все ошибки Хк связаны исключительно со случайными помехами измерению. Тогда величина Х (результат измерения) с одинаковой вероятностью может оказаться как больше
Будем считать, что среди ошибок измерения нет ошибок систематических. То есть нет ошибок, приводящих к систематическому завышению или занижению результатов измерения (из-за неотрегулированности прибора, недобросовестности измерителя, и т. д.). То есть все ошибки Хк связаны исключительно со случайными помехами измерению. Тогда величина Х (результат измерения) с одинаковой вероятностью может оказаться как больше ![]() , так и меньше
, так и меньше ![]() . При этом, в соответствии с формулой (4.5), она теоретически может принять значение Х, как угодно далеко отстоящее от
. При этом, в соответствии с формулой (4.5), она теоретически может принять значение Х, как угодно далеко отстоящее от ![]() в ту или другую сторону. Но чем дальше оно будет отстоять от
в ту или другую сторону. Но чем дальше оно будет отстоять от ![]() , тем менее вероятным оно будет. Действительно, большое отклонение Х от
, тем менее вероятным оно будет. Действительно, большое отклонение Х от ![]() - это большая итоговая ошибка измерения. А большие ошибки измерения, естественно, менее вероятны, чем малые. Очень же большие ошибки практически невероятны.
- это большая итоговая ошибка измерения. А большие ошибки измерения, естественно, менее вероятны, чем малые. Очень же большие ошибки практически невероятны.
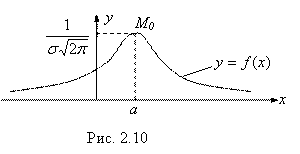
Из всего сказанного выше вытекает, что случайная величина Х, Имеющая структуру (4.5) – это непрерывная случайная величина, возможные значения которой заполняют всю числовую ось Ох. А её плотность вероятности ![]() имеет в принципе графический вид, изображенный на рис. 2.10.
имеет в принципе графический вид, изображенный на рис. 2.10.
Российский математик Ляпунов в начале 20-го века вывел аналитический вид (формулу) для этой плотности вероятности:
 (4.6)
(4.6)
Здесь ![]() - мода и одновременно математическое ожидание (среднее значение) величины Х, а
- мода и одновременно математическое ожидание (среднее значение) величины Х, а ![]() – ее среднее квадратическое отклонение (среднее отклонение Х от
– ее среднее квадратическое отклонение (среднее отклонение Х от ![]() без учета знака отклонения). То есть
без учета знака отклонения). То есть
![]() (4.7)
(4.7)
Если Х – результат измерения величины ![]() , то в формулах (4.7)
, то в формулах (4.7) ![]() - это истинное значение измеряемой величины (обычно неизвестное и подлежащее определению), а
- это истинное значение измеряемой величины (обычно неизвестное и подлежащее определению), а ![]() – среднее значение итоговой (суммарной) ошибки измерения, зависящее как от точности измерительного прибора, так и от условий измерения. Эта ошибка обычно определяется опытным путем.
– среднее значение итоговой (суммарной) ошибки измерения, зависящее как от точности измерительного прибора, так и от условий измерения. Эта ошибка обычно определяется опытным путем.
Случайная величина Х, представимая в виде (4.5), называется Распределенной нормально. То есть такая величина Х Имеет нормальное распределение. Или, что то же самое, Величина Х распределена по нормальному закону.
Нормально распределенная случайная величина Х может в принципе принять любое значение от ![]() до
до ![]() , а ее плотность вероятности имеет вид (4.6).
, а ее плотность вероятности имеет вид (4.6).
Результаты различного рода измерений – это случайные величины, распределенные приблизительно по нормальному закону. Приблизительно нормально распределенными случайными величинами будут и итоговые (суммарные) ошибки этих измерений, ибо они имеют вид (4.5) при ![]() =0. И вообще, приблизительно нормально распределенными будут все случайные величины Х, которые имели бы в каждом испытании неизменное значение
=0. И вообще, приблизительно нормально распределенными будут все случайные величины Х, которые имели бы в каждом испытании неизменное значение ![]() , если бы не незначительные случайные добавки, которых много и которые “уводят” значение величины Х от
, если бы не незначительные случайные добавки, которых много и которые “уводят” значение величины Х от ![]() в большую или в меньшую сторону.
в большую или в меньшую сторону.
Например, если станок-автомат настроен на изготовление деталей определенного размера ![]() , то реальный размер Х изготавливаемых деталей, в силу различного рода случайных факторов, будет иметь вид (4.5) и, следовательно, будет случайной величиной, распределенной приблизительно нормально.
, то реальный размер Х изготавливаемых деталей, в силу различного рода случайных факторов, будет иметь вид (4.5) и, следовательно, будет случайной величиной, распределенной приблизительно нормально.
Приблизительно нормально распределенными случайными величинами можно также считать суточный привес одного или группы животных при постоянном рационе их кормления; суточный надой одной или нескольких коров при одних и тех же условиях их содержания; расход семян на единицу засеваемой площади при неизменной технологии сева; ежедневный объем продаж магазина при неизменном в целом спросе на продукцию этого магазина, и т. д. С такого рода случайными величинами чаще всего приходится иметь дело на практике. Отсюда возник и термин для их названия – “нормально распределенные”.
Нормально распределенные случайные величины обладают важным свойством (мы докажем его в §5): если Х – нормально распределенная величина с некоторыми параметрами (![]() ;
;![]() ), то любая линейная комбинация
), то любая линейная комбинация ![]() - тоже нормально распределенная случайная величина, имеющая параметры (
- тоже нормально распределенная случайная величина, имеющая параметры (![]() ). В частности, нормально распределенная случайная величина
). В частности, нормально распределенная случайная величина
![]() (4.8)
(4.8)
Имеет параметры (![]() ) и называется Нормированной нормально распределенной случайной величиной. Ее плотность вероятности
) и называется Нормированной нормально распределенной случайной величиной. Ее плотность вероятности ![]() , согласно (4.6), имеет вид
, согласно (4.6), имеет вид
![]() (4.9)
(4.9)
То есть она представляет собой функцию Гаусса (см. (6.3), глава 1). Ее график представлен на рис. 1.4 (стр.34).
 Вид графика плотности вероятности
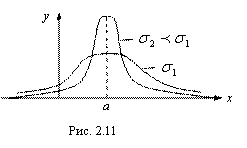
Вид графика плотности вероятности ![]() нормально распределенных случайных величин Х, согласно рис. (2.10), зависит от величины их параметров (
нормально распределенных случайных величин Х, согласно рис. (2.10), зависит от величины их параметров (![]() ). А именно, значение
). А именно, значение ![]() определяет вертикальную ось симметрии этого графика, а величина
определяет вертикальную ось симметрии этого графика, а величина ![]() определяет высоту графика: чем
определяет высоту графика: чем ![]() меньше, тем вершина
меньше, тем вершина ![]() графика выше. А чем график выше, тем он уже. Сужение графика плотности вероятности
графика выше. А чем график выше, тем он уже. Сужение графика плотности вероятности ![]() с увеличением его высоты связано с тем, что площадь между осью Ох и графиком плотности вероятности
с увеличением его высоты связано с тем, что площадь между осью Ох и графиком плотности вероятности ![]() для любой непрерывной случайной величины, согласно (3.8), должна быть равна единице. Поэтому если этот график увеличивает свою высоту, то он автоматически становится уже (рис.2.11):
для любой непрерывной случайной величины, согласно (3.8), должна быть равна единице. Поэтому если этот график увеличивает свою высоту, то он автоматически становится уже (рис.2.11):
Рассмотрим теперь следующий важный для практики вопрос: какова вероятность того, что в результате испытания нормально распределенная случайная величина Х с параметрами (![]() ;
; ![]() ) примет значение в некотором заданном числовом промежутке
) примет значение в некотором заданном числовом промежутке ![]() ? Ответ на этот вопрос мы получим с помощью формулы (3.6), которая приводит к следующему результату:
? Ответ на этот вопрос мы получим с помощью формулы (3.6), которая приводит к следующему результату:
![]() (4.10)
(4.10)
Здесь ![]() – уже известный нам интеграл вероятностей (см. главу 1, формулу (6.9) и рис. 1.5). Действительно,
– уже известный нам интеграл вероятностей (см. главу 1, формулу (6.9) и рис. 1.5). Действительно,

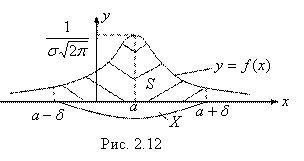
На основании полученной формулы (4.10) следует (выведите это самостоятельно), что для любого ![]()
![]() (4.11)
(4.11)
Геометрическая иллюстрация последнего равенства дана на рис.2.12.
В частности, используя формулу (4.11) и таблицу функции ![]() (фрагмент этой таблицы приведен в (6.10), глава 1), получим:
(фрагмент этой таблицы приведен в (6.10), глава 1), получим:
![]()
![]() (4.12)
(4.12)
![]()
 Последний из этих результатов означает, что Практически наверняка экспериментальное значение нормально распределенной случайной величины Х Будет содержаться в пределах
Последний из этих результатов означает, что Практически наверняка экспериментальное значение нормально распределенной случайной величины Х Будет содержаться в пределах ![]() . То есть событие, состоящее в том, что экспериментальное значение нормально распределенной случайной величины Х отклонится от её среднего значения
. То есть событие, состоящее в том, что экспериментальное значение нормально распределенной случайной величины Х отклонится от её среднего значения ![]() в ту или другую сторону больше, чем на
в ту или другую сторону больше, чем на ![]() (на три средних отклонения от среднего), практически невероятно. Этот вывод называют Правилом трех сигм.
(на три средних отклонения от среднего), практически невероятно. Этот вывод называют Правилом трех сигм.
Например, если Х – результат взвешивания некоторой массы ![]() , то
, то ![]() представляет собой среднюю ошибку взвешивания на данных весах. И если, например,
представляет собой среднюю ошибку взвешивания на данных весах. И если, например, ![]() = 5 г, то в соответствии с правилом трех сигм практически невероятно, что случайная ошибка взвешивания окажется больше 15 г (в ту или в другую сторону).
= 5 г, то в соответствии с правилом трех сигм практически невероятно, что случайная ошибка взвешивания окажется больше 15 г (в ту или в другую сторону).
Пример 2. Станок-автомат изготавливает шарики. Шарик считается годным, если отклонение Х – диаметра шарика от проектного размера по абсолютной величине не превосходит 0,7 мм. Опытным путем установлено, что ![]() =
=![]() =0,4 мм. Определить, сколько процентов годных шариков изготовляет автомат.
=0,4 мм. Определить, сколько процентов годных шариков изготовляет автомат.
Решение. Отклонение Х диаметра шарика от проектного размера – это ошибка диаметра шарика. При условии, что станок настроен правильно (систематических ошибок в работе станка нет), эта ошибка Х складывается из множества мелких случайных ошибок Хк, связанных с действием различных независимых друг от друга случайных факторов. То есть ![]() . Таким образом, ее выражение соответствует формуле (4.5) при
. Таким образом, ее выражение соответствует формуле (4.5) при ![]() = 0. А значит, Х – случайная величина, распределенная нормально с математическим ожиданием (средним значением)
= 0. А значит, Х – случайная величина, распределенная нормально с математическим ожиданием (средним значением) ![]() = 0 и средним квадратическим отклонением
= 0 и средним квадратическим отклонением ![]() = 0,4 мм (дано по условию задачи). Величина
= 0,4 мм (дано по условию задачи). Величина ![]() = 0,4 мм означает, что среднее значение отклонения ошибки Х от ее среднего значения
= 0,4 мм означает, что среднее значение отклонения ошибки Х от ее среднего значения ![]() = 0 без учета знака отклонения, то есть среднее значение самой этой ошибки, если не учитывать ее знак, составляет 0,4 мм. Иначе говоря, станок работает со средней ошибкой 0,4 мм (в ту или другую сторону).
= 0 без учета знака отклонения, то есть среднее значение самой этой ошибки, если не учитывать ее знак, составляет 0,4 мм. Иначе говоря, станок работает со средней ошибкой 0,4 мм (в ту или другую сторону).
По условию задачи, каждый изготовленный станком-автоматом шарик будет считаться годным, если ошибка Х его диаметра будет удовлетворять неравенству ![]() 0,7 мм, то есть она будет в пределах [-0,7 мм; 0,7 мм]. Найдем вероятность этого. Применяя формулу (4.11), получаем:
0,7 мм, то есть она будет в пределах [-0,7 мм; 0,7 мм]. Найдем вероятность этого. Применяя формулу (4.11), получаем:
![]()
Итак, вероятность того, что каждый изготовленный станком-автоматом шарик окажется годным, составляет 0,92. Это значит, что этот станок изготовляет в среднем 92% годных шариков.
| < Предыдущая | Следующая > |
|---|