1.22. Равномерное распределение

Определение. Непрерывная случайная величина Х называется распределенной Равномерно, если все ее возможные значения равновероятны.

Это значит, что если Х - равномерно распределенная случайная величина, и – промежуток ее возможных значений, то плотность вероятности величины Х для всех одинакова:

. (4.1)

Константа С не может быть произвольной. Ее значение должно быть таким, чтобы обеспечивалось условие (3.8). Из него следует:

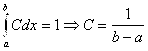(4.2)

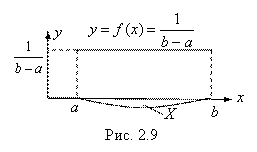
Таким образом, равномерно распределенная на отрезке непрерывная случайная величина Х имеет на нем следующую плотность вероятности (рис. 2.9):

(4.3)

А числовые характеристики этой величины таковы (получить их самостоятельно):

(4.4)

Равномерно распределенными будут, например, следующие величины:

1) Координата Х точки, бросаемой наудачу на отрезок ;

2) Ошибка Х, производимая при округлении приближенных чисел до нужного десятичного знака при производстве арифметических вычислений;

3) Время Т ожидания пассажиром троллейбуса, маршрутного такси, поезда метро и прочих средств общественного транспорта при регулярном графике их движения. И т. д.

Пример 1. При производстве арифметических вычислений их результаты округляют до сотых. Какова вероятность того, что ошибка Х, допущенная при округлении очередного числа, окажется не больше одной тысячной (без учета ее знака)?

Решение. Ошибка Х округления чисел до сотых – равномерно распределенная случайная величина, принимающая свои возможные значения (если не учитывать их знак) на промежутке [0; 0,005]. Поэтому ее плотность вероятности, согласно (4.3), будет иметь вид:

.

А тогда, используя формулу (3.6), получим и искомую вероятность:

< Предыдущая		Следующая >