1.21. Числовые характеристики непрерывных случайных величин

Рассмотрим теперь вопрос об основных числовых характеристиках (; ; ; ) непрерывной случайной величины . Этим числовым характеристикам придадим тот же смысл, какой они имели в §1 для дискретных случайных величин:

; ;

; (3.9)

Начнем с – с математического ожидания величины . Найти – это значит найти среднее значение величины . Для его нахождения разобьем мысленно отрезок всех возможных значений непрерывной случайной величины на бесконечно большое число бесконечно малых участков с длинами , и на каждом из них выберем некоторую произвольную точку . Попадание значения На каждый из этих участков – это фактически, в силу их бесконечной малости, попадание в соответствующую точку , осуществляемое с вероятностью (см. (3.4)). Поэтому, в соответствии с формулой (1.4), получаем:

(3.10)

То есть, получаем окончательно:

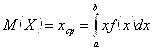(3.11)

Опираясь на полученную формулу для математического ожидания непрерывной случайной величины и используя определение (3.9) дисперсии величины , получим формулу для вычисления :

(3.12)

После раскрытия квадрата разности, разбиения интеграла (3.12) на три интеграла и учете равенств (3.8) и (3.11) получим так называемую Упрощенную формулу для дисперсии :

(3.13)

Здесь

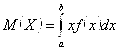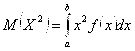; (3.14)

– математические ожидания величин и соответственно. Кстати, упрощенная формула (3.13) для дисперсии непрерывной случайной величины полностью совпадает с аналогичной формулой (1.25) для дисперсии дискретной случайной величины. Формулы (3.9) для среднего квадратического отклонения и коэффициента вариации непрерывной случайной величины тоже полностью совпадают с аналогичными формулами (1.21) и (1.27) для дискретной случайной величины. И смысл всех этих числовых характеристик для обеих случайных величин полностью совпадает.

Примечание. Если интервал возможных значений непрерывной случайной величины бесконечен (в одну или в обе стороны), то интегралы (3.12) и (3.14) будут несобственными и могут оказаться расходящимися – то есть не дадут конечных значений (дадут или ). Тогда , , а вместе с ними , могут не иметь конечных значений.

Пример 1. Непрерывная случайная величина Имеет возможные значения, заполняющие отрезок оси , а ее плотность вероятности – это линейная функция вида

(3.15)

А) Найти ; б) Построить график функции ; в) Найти и ; г) Найти , , , .

Решение. а) Неизвестную константу найдем из условия (3.8):

Таким образом, плотность вероятности

(3.16)

Б) Построим график функции – график плотности вероятности рассматриваемой непрерывной случайной величины (рис. 2.7). Судя по этому графику, наиболее вероятным значением величины (модой ) является значение .

в) Найдем вероятность , то есть вероятность попадания значения в левую половину отрезка . Для этого используем формулу (3.6):

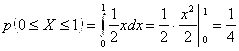Аналогично найдем вероятность того, что попадет в правую половину отрезка :

Таким образом, вероятность попадания значения случайной величины в правую половину отрезка втрое больше, чем вероятность ее попадания в левую половину этого же отрезка. Это произошло потому, что возможные значения величины правой половины отрезка вероятнее значений левой половины (см. рис. 2.7). Отметим, что найденные вероятности и в сумме, как и положено, дают единицу.

Г) Найдем числовые характеристики (; ; ; ) величины :

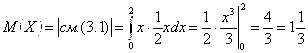Таким образом, – среднее значение величины . Оно находится не в середине отрезка , а правее, что совершенно естественно, ибо в правой половине отрезка содержатся более вероятные значения , чем в его левой половине.

Теперь найдем дисперсию . Предварительно найдем :

Значит, согласно (3.13)

А теперь найдем оставшиеся две числовые характеристики величины X:

Среднее квадратическое отклонение показывает, что среднее отклонение величины Х от ее среднего значения составляет (без учета знака отклонения) приблизительно 0,47. А коэффициент вариации показывает, что по отношению к среднему значению это отклонение составляет приблизительно 35%.

Для непрерывных случайных величин, как и для дискретных, можно ввести понятия суммы и произведения.

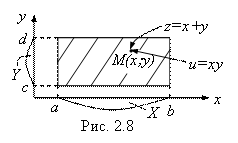Пусть X и Y – некоторые две непрерывные случайные величины, причем [A; B] и - промежуток возможных значений и плотность вероятности величины Х, а [C; D] и - соответствующие характеристики величины Y. Тогда сумма – непрерывная случайная величина, которая в качестве своих возможных значений принимает всевозможные суммы значений величин X и Y. А произведение - непрерывная случайная величина, которая в качестве своих возможных значений принимает всевозможные произведения значений X и Y (рис. 2.8). Таким образом, возможные значения и величин и комбинируются из координат (X; Y) точек заштрихованного на рис.2.8 прямоугольника. А, следовательно, и плотности вероятности обеих этих величин комбинируются из плотностей вероятностей и величин X И Y. Комбинации эти выглядят сложно, особенно если случайные величины X и Y являются зависимыми друг от друга, поэтому приводить их не будем. Тем более, что для нахождения числовых характеристик случайных величин и Без них зачастую можно и обойтись (это следует из приводимых ниже свойств сумм и произведений случайных величин).

Если случайные величины X и Y Независимы, то каждая из них принимает свои возможные значения вне всякой связи с возможными значениями другой величины. Если же это не так, то случайные величины X И Y являются Зависимыми. Кстати, смысл зависимости – независимости случайных величин полностью аналогичен смыслу зависимости – независимости случайных событий (см. §3 главы 1).

Для непрерывных случайных величин имеют место те же свойства, что и для дискретных случайных величин (§1). А именно:

1. Для любых непрерывных случайных величин X и Y

(3.17)

2. Для любых непрерывных случайных величин X и Y

(3.18)

В частности, так как для любой константы С (см.(1.5)), то

(3.19)

3. Если непрерывные случайные величины X и Y независимы, то

(3.20)

4. Для любой непрерывной случайной величины Х и любой константы С

(3.21)

5. Если непрерывные случайные величины X и Y независимы, то

; (3.22)

В частности, так как (см.(1.28)) и так как любая непрерывная случайная величина и любая константа независимы, то

(3.23)

Приведенные выше свойства для двух случайных величин переносятся и на несколько случайных величин:

1. Для любых непрерывных случайных величин (Х1; Х2; … Хр)

(3.24)

2. Если непрерывные случайные величины (Х1; Х2; … Хр) взаимно независимы, то

(3.25)

3. Если непрерывные случайные величины (Х1; Х2; … ХР) взаимно независимы, то

(3.26)

Упражнения

1. Когда непрерывная случайная величина считается заданной? Какие имеются ограничения при задании непрерывных случайных величин? Как называются основные числовые характеристики непрерывной случайной величины, как они находятся и каков их смысл?

2. Непрерывная случайная величина Х может принять любое значение Х от до . Ее плотность вероятности .

А) Найти С; б) Построить график функции ; в) Найти числовые характеристики , , , величины Х.

Ответ: а) ; в) ; ; ; - не имеет смысла.

3. Муж и жена работают на сдельной работе и на разных предприятиях. То есть их месячные зарплаты X и Y – независимые случайные величины. Известно, что = 5000 руб.; =4000 руб.; =500 руб.; =200 руб. Найти для их совместной суммарной зарплаты Z=X+Y: а) ; б) ; в) ; г) .