1.20. Непрерывные случайные величины и их числовые характеристики

Пусть – непрерывная случайная величина, возможные значения которой заполняют сплошь (непрерывно) некоторый промежуток Числовой оси (рис. 2.2). Для полной характеристики этой величины недостаточно, очевидно, задать только этот промежуток ее возможных значений. Нужно еще как-то указать, насколько возможно (вероятно) каждое из этих значений. Сделать это так, как это делалось для дискретных случайных величин, то есть с помощью закона распределения (таблицы), в которой одно за другим перечислены все возможные значения случайной величины и указаны их вероятности, очевидно, невозможно. Для непрерывной случайной величины это делается иначе – с помощью так называемой Плотности вероятности.

Введем это важное понятие. Пусть – одно из возможных значений непрерывной случайной величины . Окружим это значение некоторым малым промежутком длиной (окрестностью Точки ). И пусть – вероятность того, что в результате испытания величина примет значение, принадлежащее этой окрестности (попадет в эту окрестность) – рис. 2.4. 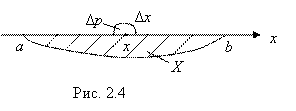Если мы теперь найдем отношение то получим вероятность, приходящуюся В среднем на единицу длины участка . То есть получим Среднюю линейную плотность вероятности непрерывной случайной величины на участке . А теперь в отношении перейдем к пределу при (при этом и ). При таком предельном переходе отрезок будет стягиваться в точку , и в пределе получим истинную линейную плотность вероятности величины Х в самой точке . Ее обозначим символом

или (3.1)

И будем называть Плотностью вероятности непрерывной случайной величины в точке . В последнем равенстве (3.1) – это длина бесконечно малого промежутка, окружающего точку , а – это бесконечно малая вероятность попадания значения величины на этот бесконечно малый промежуток.

Ясно, что плотность вероятности неотрицательна для любого , ибо сама вероятность по природе своей неотрицательна:

(3.2)

Если у непрерывной случайной величины задан промежуток (или интервал ) ее возможных значений, а также задана ее плотность вероятности для всех , принадлежащих этому промежутку или интервалу, то непрерывная случайная величина считается заданной.

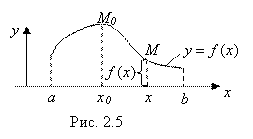Отметим, что если мы построим график плотности вероятности , то получим возможность наглядно сравнивать вероятности различных возможных значений Х Случайной величины(рис. 2.5).

Действительно, согласно своего определения (3.1), плотность вероятности , вычисленная в точке , показывает, какой была бы вероятность попадания значения случайной величины На единицу длины отрезка , если бы все значения этой величины были столь же вероятны, что и данное значение . В этом смысле плотность вероятности совершенно аналогична, например, линейной плотности вещества материального отрезка (материальной нити), если вещество распределено вдоль этого отрезка. Указанную линейную плотность вещества для различных значений мы опять вычисляли бы по формуле (3.1), только была бы не вероятность, а масса отрезка . И ее числовое значение в выбранной точке ( например, ) означало бы, что если бы вещество было распределено вдоль отрезка равномерно и столь же плотно, что и в точке (нить на всем своем протяжении имела бы ту же толщину, что и в точке ), то масса каждой единицы длины (каждого сантиметра) отрезка составляла бы единиц массы ().

Итак, смысл плотности вероятности выяснен. Если при изменении меняется и величина (как на рис. 2.5), то более вероятны те значения , для которых больше. И во столько раз более вероятны, во сколько раз больше их плотность вероятности . В частности, на рис. 2.5 наиболее вероятным значением величины на отрезке является значение , а наименее вероятным – значение . Можно даже зрительно и оценить, во сколько раз значение вероятнее значения (раза в три).

Наиболее вероятное значение случайной величины (как непрерывной, так и дискретной) называется Модой (обозначается ). Для непрерывной случайной величины , представленной на рис.2.5,

Мода величины , как наиболее вероятное ее значение, при повторных испытаниях встречается чаще других ее значений. Отсюда и название: мода.

А теперь получим в некотором смысле парадоксальный вывод: у непрерывной случайной величины все ее возможные значения имеют нулевую вероятность!

Действительно, из (3.1) следует:

3.4)

Здесь – это бесконечно малая вероятность того, что случайная величина Попадет в бесконечно малую окрестность точки . В этой окрестности, несмотря на ее бесконечную малость, кроме точки содержится еще бесконечно много других точек. Если сузить указанную окрестность до одной точки , то в этом случае , а значит, и . И эта – вероятность того, что . То есть действительно

(3.5)

То, что все возможные значения непрерывной случайной величины имеют нулевую вероятность – еще не значит, что эта величина не может принять то или иное свое значение. Ведь в каждом испытании случайная величина какое-то значение примет. Значит, в принципе она может принять любое из своих возможных значений. Просто этих возможных значений у нее бесконечно много, поэтому для каждого возможного значения имеется лишь один шанс быть принятым против бесконечного числа шансов быть не принятым. Отсюда и следует нулевая вероятность для каждого возможного значения непрерывной случайной величины . Но шанс этот все-таки есть!

Далее: нулевые вероятности различных значений непрерывной случайной величины в сумме должны давать единицу! Действительно, указанная сумма вероятностей всех возможных значений величины – это вероятность того, что величина примет одно из этих своих значений. А это – достоверное событие, вероятность которого, как известно, равна единице. Ну, а то, что из бесконечного числа нулей в сумме получается единица – так точно так же из бесконечного числа точек, не имеющих размера (имеющих нулевой размер) складываются реальные отрезки, материальные тела и т. д.

Несмотря на нулевые вероятности возможных значений непрерывной случайной величины , эти нулевые вероятности, как указывалось выше, можно сравнивать (с помощью плотности вероятности ). Те значения , для которых больше, и вероятность имеют большую (одна нулевая вероятность больше другой!). То есть с помощью плотности вероятности сравниваются весомости тех единственных шансов быть принятыми, которые есть у каждого возможного значения величины . В частности, на рис. 2.5 самым весомым этот шанс является у значения – моды величины . Указанное сравнение нулевых вероятностей совершенно аналогично сравнению нулевых масс отдельных точек разных веществ. Например, совершенно естественно считать, что отдельно взятая точка свинца имеет нулевую массу, но большую, чем нулевая масса отдельно взятой точки алюминия, ибо при одном и том же количестве точек (при одном и том же объеме) масса свинца больше массы алюминия. И сравнивать количественно нулевые массы отдельных точек разных веществ можно по плотности этих веществ: во сколько раз плотность свинца больше плотности алюминия, во столько же раз точка свинца массивнее точки алюминия.

При исследовании непрерывных случайных величин одной из основных задач является задача нахождения вероятности того, что в результате испытания заданная непрерывная случайная величина примет значение, содержащееся в некоторой заданной части промежутка . Эта вероятность находится по формуле:

(3.6)

Иначе говоря,

, (3.7)

Где – площадь вертикальной полосы, изображенной на рис. 2.6:

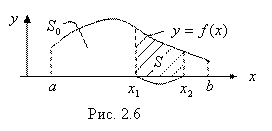Докажем формулу (3.7). Для этого мысленно разобьем отрезок на бесконечно малые участки с длинами и выберем внутри каждого такого участка некоторую точку . Тогда вероятность попадания значения на каждый из таких участков найдется по формуле (3.4). Попадание же значения На отрезок равносильно попаданию этого значения хотя бы на один из указанных участков . Попадание значения величины На различные участки – это попарно несовместные случайные события. Поэтому по формуле сложения вероятностей попарно несовместных событий (по формуле (4.10) главы 1) получаем:

.

Формула (3.6) доказана. А вспоминая геометрический смысл определенного интеграла, приходим и к формуле (3.7).

Так как как вероятность достоверного события, то из формул (3.6) и (3.7) как частный случай следует:

(3.8)

Здесь площадь – площадь всей криволинейной Трапеции, расположенной между осью и графиком плотности вероятности для .

Из равенства (3.8) следует, что плотность вероятности любой непрерывной случайной величины нельзя задавать произвольно. При ее задании обязательно должны быть выполнены два вытекающих из ее смысла условия: (3.2) и (3.8). В остальном она может быть какой угодно.

< Предыдущая		Следующая >