1.25. Распределение Стьюдента (Т - распределение)

Пусть – нормированная нормально распределенная случайная величина (), а – независимая от величина, распределенная по закону с степенями свободы. Тогда величина

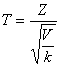(4.16)

Имеет распределение, которое называют Т- распределением, или распределением Стьюдента (псевдоним английского статистика Госсета) с степенями свободы. Очевидно, что случайная величина Т может принимать любые значения T от до . А ее плотность вероятности имеет вид:

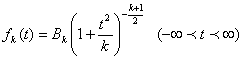(4.17)

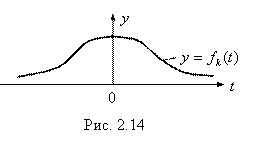График плотности вероятности Случайной величины Т, имеющей распределение Стьюдента с степенями свободы, для любого ≥1 в принципе имеет вид, изображенный на рис 2.14. Эта кривая, если сравнивать её с плотностью вероятности нормированного нормального распределения (с функцией Гаусса, рис. 1.4), ниже последней и убывает медленнее.

Очевидно, что . При этом (можно доказать) дисперсия . При

(4.18)

То есть при распределение Стьюдента стремится к нормированному нормальному распределению. Причем стремится быстро, так что при K>30 вместо распределения Стьюдента можно пользоваться нормированным нормальным распределением.

< Предыдущая		Следующая >