1.13. Повторение испытаний. Формулы Бернулли, Лапласа, Пуассона
Пусть А – случайное событие, вероятности появления и непоявления
Которого для некоторого испытания известны:
![]() ;
; ![]() ;
; ![]() (6.1)
(6.1)
И пусть производится не одно, а N повторных испытаний (или, что одно и то же, испытание повторяется N раз). Возникает естественный вопрос: какова вероятность того, что событие А В этих N повторных испытаниях появится K раз (целое число K можно задавать любым в пределах от 0 до N)? При этом не важно, в каком порядке событие А появится K раз в N испытаниях. Важно лишь общее число K Появлений этого события. Эту вероятность обозначают символом ![]() (
(![]() - вероятность того, что в N испытаниях событие А Наступит K раз). И находится она по формуле Бернулли (Яков Бернулли – швейцарский математик 17-го века):
- вероятность того, что в N испытаниях событие А Наступит K раз). И находится она по формуле Бернулли (Яков Бернулли – швейцарский математик 17-го века):
![]() (6.2)
(6.2)
Доказательство. Если в N повторных испытаниях событие А появится K Раз, то соответственно оно не появится N-K раз. И тогда вероятность любой конкретной комбинации K появлений события А и N-K непоявлений этого события можно найти по формуле (4.15) произведения вероятностей независимых в совокупности событий. То есть она равна ![]() . Таких конкретных комбинаций будет, очевидно, столько, сколько существует сочетаний из N элементов (номеров испытаний) по K элементов в каждом сочетании. Эти сочетания образуются из K номеров тех испытаний, в которых будет появляться событие А. Каждому такому сочетанию K номеров будет соответствовать единственное сочетание тех N-K номеров испытания, в которых событие А не будет появляться. Так как всего таких сочетаний
. Таких конкретных комбинаций будет, очевидно, столько, сколько существует сочетаний из N элементов (номеров испытаний) по K элементов в каждом сочетании. Эти сочетания образуются из K номеров тех испытаний, в которых будет появляться событие А. Каждому такому сочетанию K номеров будет соответствовать единственное сочетание тех N-K номеров испытания, в которых событие А не будет появляться. Так как всего таких сочетаний ![]() , и каждое из них несовместно с любым другим сочетанием, то по формуле (4.10) сложения вероятностей попарно несовместных событий искомая вероятность равна величине
, и каждое из них несовместно с любым другим сочетанием, то по формуле (4.10) сложения вероятностей попарно несовместных событий искомая вероятность равна величине ![]() , взятой
, взятой ![]() раз. В итоге и приходим к формуле Бернулли (6.2).
раз. В итоге и приходим к формуле Бернулли (6.2).
Пример 1. Монету подбрасывают пять раз подряд. Какова вероятность того, что при этом герб выпадет ровно три раза?
Решение. Будем считать испытанием однократное подбрасывание монеты. Тогда N=5 – число повторных испытаний. Далее, будем считать событием А в каждом испытании (при каждом бросании монеты) выпадение герба. Тогда
![]() ;
; ![]() ; N=5; K=3;
; N=5; K=3; ![]()
На основании формулы Бернулли получаем:
![]()
![]() .
.
Формула Бернулли – точная формула. Однако при больших значениях N (большом числе испытаний) вычисления по ней становятся громоздкими из-за необходимости вычисления факториалов больших чисел и степеней с большими показателями. В процессе этих вычислений неизбежно придется производить округления, что приведет к погрешности при определении искомой вероятности ![]() . Причем к погрешности тем большей, чем больше будет значение N (числа испытаний). В связи с этим из формулы Бернулли выведены упрощенные приближенные формулы для
. Причем к погрешности тем большей, чем больше будет значение N (числа испытаний). В связи с этим из формулы Бернулли выведены упрощенные приближенные формулы для ![]() , которые, кстати, тем точнее, чем больше число N.
, которые, кстати, тем точнее, чем больше число N.
Одна из этих приближенных формул – Локальная формула Лапласа:
![]() где
где ![]()
![]() (6.3)
(6.3)
 Функция
Функция ![]() Называется функцией вероятностей (или функцией Гаусса). График функции
Называется функцией вероятностей (или функцией Гаусса). График функции ![]() имеет вид, изображенный на рис. 1.4.
имеет вид, изображенный на рис. 1.4.
Для ![]() значение функции
значение функции ![]() Можно взять в таблице, содержащейся во многих пособиях по теории вероятностей. Приведем небольшой фрагмент этой таблицы:
Можно взять в таблице, содержащейся во многих пособиях по теории вероятностей. Приведем небольшой фрагмент этой таблицы:
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
|
J(x) |
0,3989 |
0,2420 |
0,0540 |
0,0044 |
0,0001 |
» 0 |
Для отрицательных значений X используют четность функции ![]() :
: ![]() Для X<-5 и X>5 значение
Для X<-5 и X>5 значение ![]() На практике локальную формулу Лапласа применяют, если
На практике локальную формулу Лапласа применяют, если
![]() (6.5)
(6.5)
Это условие обеспечивает приближенное нахождение вероятности ![]() с точностью до процента. Доказательство локальной формулы Лапласа опускаем.
с точностью до процента. Доказательство локальной формулы Лапласа опускаем.
Пример 2. Монету подбрасывают 100 раз подряд. Какова вероятность того, что при этом герб выпадет ровно 40 раз?
Решение. Будем считать испытанием однократное подбрасывание монеты. Тогда N=100 – число повторных испытаний. Будем считать событием А в каждом испытании (при каждом бросании монеты) выпадение герба. Тогда
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ?
?
Формулу Бернулли для подсчета искомой вероятности ![]() применять не будем – слишком велико число испытаний N (N=100). А так как
применять не будем – слишком велико число испытаний N (N=100). А так как ![]() , то вместо формулы Бернулли (6.2) применим локальную формулу Лапласа (6.3):
, то вместо формулы Бернулли (6.2) применим локальную формулу Лапласа (6.3):
![]()
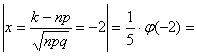
=│учтем, что ![]() │=0,0108
│=0,0108
Другой приближенной формулой для подсчета вероятностей ![]() , применяемой при больших N, является Формула Пуассона (формула редких событий):
, применяемой при больших N, является Формула Пуассона (формула редких событий):
![]()
![]() , где
, где ![]() (6.6)
(6.6)
Она применяется, когда N Велико (условно N![]() 50), а Р мало (0<Р<0,1), и когда Npq<10. То есть когда не оправдано ни применение формулы Бернулли, ни применение локальной формулы Лапласа. При этих условиях приближенная формула Пуассона, как и локальная формула Лапласа, обеспечивает определение искомой вероятности
50), а Р мало (0<Р<0,1), и когда Npq<10. То есть когда не оправдано ни применение формулы Бернулли, ни применение локальной формулы Лапласа. При этих условиях приближенная формула Пуассона, как и локальная формула Лапласа, обеспечивает определение искомой вероятности ![]() С погрешностью в пределах одного процента.
С погрешностью в пределах одного процента.
Кстати, так как вероятность![]() события А Мала (0<Р<0,1), то при повторении испытаний событие А наступает редко. Поэтому формула Пуассона и называется формулой редких событий. Вывод этой формулы опустим.
события А Мала (0<Р<0,1), то при повторении испытаний событие А наступает редко. Поэтому формула Пуассона и называется формулой редких событий. Вывод этой формулы опустим.
Пример 3. Производится 50 повторных испытаний, причем вероятность появления некоторого события А В каждом из них равна 0,98. Определить вероятность того, что событие А наступит во всех 50 испытаниях.
Решение. В данной задаче
P(A)=P=0,98; P(Ā)=Q=0,02; N=50; K=50; ![]()
Если применить формулу Бернулли, то получим результат, который очевиден и без формулы Бернулли:
![]()
Попробуем избежать громоздкой процедуры возведения числа 0,98 в 50-ую степень (её, впрочем, можно и избежать, если использовать логарифмы). То есть заменим формулу Бернулли на локальную формулу Лапласа или Пуассона.
Так как Npq=50·0,98·0,02=0,98<10, то локальную формулу Лапласа применять нельзя - мы получим слишком грубый (неточный) результат. Но и формулу Пуассона (формулу редких событий) мы тоже применить не можем, так как вероятность Р не мала, а наоборот, велика. Но зато мала вероятность Q непоявления этого события. В связи с этим переформулируем задачу: найдем вероятность ![]() того, что событие
того, что событие ![]() появится 0 раз (ни разу). Эта вероятность, очевидно, совпадает с искомой вероятностью
появится 0 раз (ни разу). Эта вероятность, очевидно, совпадает с искомой вероятностью ![]() Того, что событие А появится во всех 50 испытаниях. Тогда в этой постановке получаем:
Того, что событие А появится во всех 50 испытаниях. Тогда в этой постановке получаем:
P(Ā)=P=0,02; P(A)=Q=0,98; N=50; K=0; ![]() ?
?
Применяя формулу Пуассона (теперь ее применять можно), получим:
![]() ≈
≈![]()
![]() = |λ=Np=50·0,02=1| =
= |λ=Np=50·0,02=1| = ![]() =
=![]() ≈
≈![]() ≈ 0,37.
≈ 0,37.![]()
Рассмотрим теперь следующую задачу: какова вероятность ![]() того, что в N повторных испытаниях число K появлений события А Окажется в заданных числовых пределах [K1; K2]?
того, что в N повторных испытаниях число K появлений события А Окажется в заданных числовых пределах [K1; K2]?
Решение этой задачи очевидно:
![]() =
=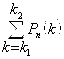 (6.7)
(6.7)
Действительно, число K окажется в пределах [K1; K2], если оно будет равно или K1, или K1+1, или K1+2, … или K2. События, приводящие к таким значениям K, друг с другом (попарно) несовместимы. А тогда по формуле (4.10) сложения вероятностей попарно несовместных событий мы и приходим к формуле (6.7).
Пример 4. Монета бросается 5 раз. Какова вероятность того, что при этом герб выпадет не более четырех раз?
Решение. Будем считать испытанием однократное бросание монеты. Тогда N=5-число повторных испытаний. А событием А в каждом испытании будем считать выпадение герба. Тогда:
р(A)=P=![]() ; Р(Ā)=Q=
; Р(Ā)=Q=![]() ; N=5; 0≤K≤4;
; N=5; 0≤K≤4; ![]()
Применяя формулу (6.7), получим:
![]()
![]() =
=![]()
Для подсчета каждого из этих пяти слагаемых следует, очевидно, применить формулу Бернулли (6.2) и полученные числа сложить.
Однако эту задачу можно решить и гораздо проще - через противоположное событие:
![]()
Если число N Испытаний велико, границы [K1; K2] широкие и если, кроме того, Npq>10, то вместо точной формулы (6.7), использование которой становится громоздким, используют Приближенную интегральную формулу Лапласа:
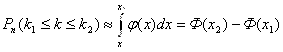 (6.8)
(6.8)
Здесь:
 ;
;  ;
;
![]()
![]() (6.9)
(6.9)
Функция ![]() - это уже известная нам функция Гаусса (её график изображен на рис. 1.4), а функция
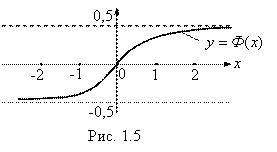
- это уже известная нам функция Гаусса (её график изображен на рис. 1.4), а функция ![]() называется Интегралом вероятностей. График этой функции изображен на рисунке 1.5. В любом пособии по теории вероятностей имеются таблицы значений интеграла вероятностей
называется Интегралом вероятностей. График этой функции изображен на рисунке 1.5. В любом пособии по теории вероятностей имеются таблицы значений интеграла вероятностей ![]() , который, как и функция Гаусса, принадлежит к числу важнейших функций теории вероятностей. Эти таблицы составлены для 0≤X ≤5. Приведем небольшой фрагмент этой таблицы:
, который, как и функция Гаусса, принадлежит к числу важнейших функций теории вероятностей. Эти таблицы составлены для 0≤X ≤5. Приведем небольшой фрагмент этой таблицы:
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
|
Ф(x) |
0 |
0,3413 |
0,4772 |
0,49865 |
0,499968 |
0,499997 |
 Для X>5 можно считать
Для X>5 можно считать ![]() =0,5. Для X<0 следует использовать нечетность функции
=0,5. Для X<0 следует использовать нечетность функции ![]() :
: ![]() .
.
Пример 5. Монету подбрасывают 100 раз подряд. Какова вероятность того, что при этом герб выпадет от 40 до 60 раз?
Решение. Будем считать испытанием однократное подбрасывание монеты. Тогда N=100 - число повторных испытаний. Событием А В каждом испытании будем считать выпадение герба. Тогда:
р(А)=р=![]() ; Р(Ā)=Q=
; Р(Ā)=Q=![]() ; N=100; 40≤K≤60;
; N=100; 40≤K≤60; ![]() =?
=?
Так как Npq=25>10, то применим интегральную формулу Лапласа:
![]()
![]() ;
; ![]() ;
;
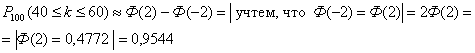
Упражнения
1. Показать, что наиболее вероятным числом появления события А в N повторных испытаниях является число KНаив.=Np (или ближайшее к Np целое число, если Np не целое).
2. Два равносильных игрока играют в игру, ничьи в которой исключаются. Какова вероятность для первого игрока выиграть: а) одну партию из двух? б) две из четырех? в) три из шести?
Ответ: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]()
3. Отрезок АВ разделен точкой С в отношении 2:1. На этот отрезок наудачу брошены четыре точки. Найти вероятность того, что две из них окажутся левее точки С, а две - правее.
Ответ: ![]()
4.Вероятность рождения мальчика равна 0,515. Найти вероятность того, что среди 100 новорожденных мальчиков и девочек окажется поровну.
Ответ: 0,07
5. Магазин получил 500 бутылок в стеклянной таре. Вероятность того, что при перевозке любая из бутылок окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) менее двух; в) не менее двух; г) хотя бы одну.
Ответ: а) 0,22; б) 0,20; в) 0,80; г) 0,95
6. Автомобильный завод выпускает 80% автомобилей без существенных дефектов. Какова вероятность того, что среди 600 автомобилей, поступивших с завода на автомобильную биржу, окажется не менее 500 автомобилей без существенных дефектов?
Ответ: 0,02
7. Сколько раз нужно бросить монету, чтобы с вероятностью 0,95 можно было ожидать, что относительная частота ![]() появлений герба отклонится от вероятности Р=0,5 появления герба при одном бросании монеты не более, чем на 0,02?
появлений герба отклонится от вероятности Р=0,5 появления герба при одном бросании монеты не более, чем на 0,02?
Ответ: N ≥ 2401.
| < Предыдущая | Следующая > |
|---|