1.14. Случайные величины

Вторым основным понятием теории вероятностей, наряду с понятием случайного события, является понятие Случайной величины (случайного числа).

Определение 1. Величина Х называется Случайной, если в результате испытания (измерения) она примет значение, которое заранее неизвестно и которое зависит от случайных причин, учесть которые заранее невозможно.

Например, оценка, которую студент получит на предстоящем экзамене - случайная величина; сумма выигрыша в лотерею – случайная величина; ошибка измерения, допускаемая измерительным прибором – случайная величина, и т. д.

Не следует путать случайное событие со случайной величиной. Например, сдача экзамена – это случайное событие, а оценка на экзамене – случайная величина; выигрыш в лотерею – случайное событие, а сумма выигрыша – случайная величина, и т. д.

Случайные величины делятся на два основных класса - Дискретные и непрерывные.

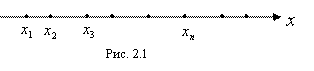Определение 2. Случайная величина называется Дискретной (прерывистой), если её возможные значения, нанесенные на числовую ось, выглядят на ней в виде отдельных, изолированных друг от друга, точек (х1; х2; х3; …), которые можно пронумеровать (рисунок 2.1). Число этих возможных значений (Х1; х2; х3; …) дискретной случайной величины Х может быть как конечным, так и бесконечным.

Пример 1. Оценка Х, которую получит студент на предстоящем экзамене – дискретная случайная величина. Действительно, её возможные значения (2, 3, 4, 5) на числовой оси представляются в виде отдельных, изолированных друг от друга, точек. Их число, кстати, конечно (равно четырем).

Пример 2. Число вызовов, поступающих за некоторое время (например, за сутки) на телефонную станцию – дискретная случайная величина Х. Действительно, её возможные значения (0; 1; 2; 3; …) – это отдельные, изолированные друг от друга, точки числовой оси. Их число, заметим, теоретически бесконечно.

Определение 2. Случайная величина Х называется Непрерывной, если она может принять любое значение х из некоторого числового промежутка [A; B] или интервала (A; B) числовой оси (конечного или бесконечного).

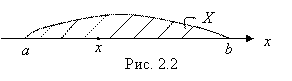Таким образом, возможные значения непрерывной случайной величины Х Заполняют Сплошь (Непрерывно) некоторый промежуток или интервал числовой оси (рисунок 2.2). При этом предполагается, что вероятность принятия величиной Х Своего значения на любом бесконечно малом участке этого промежутка или интервала Бесконечно мала.

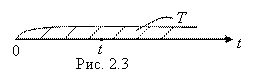Пример3. Время Т Работы некоторого механизма или устройства до очередного сбоя (поломки) – непрерывная случайная величина. Действительно, её возможные значения T заполняют сплошь положительную часть оси времени T (рисунок 2.3), ибо механизм может выйти из строя в любой момент времени T (T > 0). При этом вероятность того, что он выйдет из строя в течении любого бесконечного малого промежутка времени, очевидно, бесконечно мала.

< Предыдущая		Следующая >