11. Бином Ньютона

Название биномиальных коэффициентов следует из теоремы, известной в математике как Формула Бинома Ньютона.

Теорема 11.1. .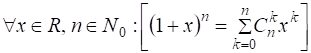

Теорема 11.2. .

Доказательство. По формуле бинома с использованием тождественных преобразований алгебраических выражений.

.■

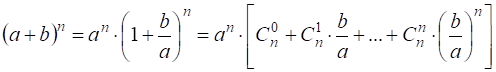
Последнее равенство также называется формулой бинома Ньютона, его правая часть называется разложением степени бинома.

Теорема 11.3.

Доказательство следует из формулы бинома Ньютона при

Теорема 11.4.

Доказательство следует из формулы бинома Ньютона при .

Формулы сокращённого умножения являются частными случаями формулы бинома Ньютона.

1) квадрат суммы при :

;

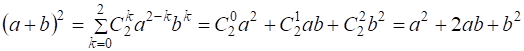Заменив в формуле квадрата суммы B на (–B), получаем формулу квадрата разности:

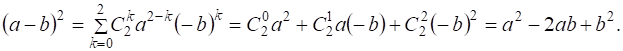
2) куб суммы при :

заменив в формуле куба суммы B на (–B), получаем формулу куба разности:

Задачи и упражнения.

11.1. Найдите разложение бинома.

11.2. Найдите член разложения бинома , не содержащий Х.

11.3. Найдите наибольший коэффициент разложения бинома , если сумма всех коэффициентов равна 4096.

11.4. Найдите Х в 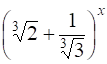, если отношение седьмого слагаемого от начала в разложении бинома к седьмому слагаемому от конца равно .

11.5. Докажите, что сумма квадратов коэффициентов разложения бинома равна .

12. Треугольник Паскаля.

Для вычисления биномиальных коэффициентов используется специальная таблица.

Таблица 2

Вычисление биномиальных коэффициентов

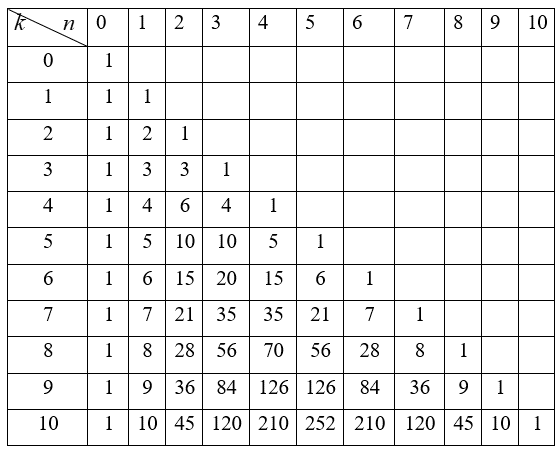
Биномиальные коэффициенты удобно выстроить в Треугольник Паскаля – равнобедренный треугольник, обладающий следующими закономерностями:

1) в строке треугольника записываются биномиальные коэффициенты -й степени бинома;

2) число располагается в строке на месте;

3) боковые стороны треугольника состоят только из единиц;

4) каждое внутреннее число строки равно сумме двух последовательных чисел предыдущей строки, стоящих над ним слева и справа.

На рисунке 7 представлен треугольник Паскаля, выстроенный для коэффициентов разложения бинома -й степени.

Рис. 1

Треугольник Паскаля

Например, при треугольник Паскаля имеет вид:

Значит, .

Задачи и упражнения.

12.1. Найдите разложение бинома.

12.2. Докажите, что .

12.3. Проверьте выполнение равенства задачи 3.27 для 8 и 10 строк треугольника Паскаля.

< Предыдущая		Следующая >