13. Рекуррентные соотношения

Рассмотрим последовательность элементов , первые элементов которой известны.

Всякую конечную последовательность элементов можно рассматривать как бесконечную, считая все её элементы, начиная с некоторого номера, равными нулю.

Определение. Рекуррентным соотношением между элементами последовательности называется формула вида ,.

Например, рекуррентное соотношение , , задает Последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8,…

Для вычисления любого элемента последовательности с помощью заданного рекуррентного соотношения требуется вычисление всех предыдущих её элементов. Если заданная последовательность элементов удовлетворяет линейному рекуррентному соотношению, то решение задачи об отыскании общей формулы вычисления аналогично решению линейных дифференциальных уравнений высших порядков с постоянными коэффициентами.

Рассмотрим последовательность элементов . - известные начальные значения последовательности элементов, удовлетворяющих линейному неоднородному рекуррентному соотношению (1):

, (1)

- известные действительные числа.

Тогда (2) – линейное однородное рекуррентное соотношение, соответствующее (1):

. (2)

Определение. Характеристическим Уравнением, соответствующим (2), называется уравнение вида

. (3)

Корни уравнения (3) называются характеристическими числами рекуррентного соотношения (1).

Теорема 13.1. (О структуре общего решения линейного неоднородного рекуррентного соотношения (1)). Пусть общее решение линейного однородного рекуррентного соотношения (2), - Любое частное решение линейного неоднородного рекуррентного соотношения (1). Тогда - общее решение линейного неоднородного рекуррентного соотношения (1).

Теорема 13.2. (О структуре общего решения линейного однородного рекуррентного соотношения (2)). Если - действительный корень характеристического уравнения (3) кратности , то общее решение линейного однородного рекуррентного соотношения (2) вычисляется по формул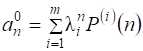е , где - многочлен степени по переменной N, . Коэффициенты определяются из начальных значений рекуррентного соотношения.

Общее решение рекуррентного соотношения (2) при и действительных корнях уравнения (3) и имеет вид

при ,

при =.

Пример. Выведем формулу Бине для вычисления последовательности чисел Фибоначчи.

Решение. ,

- линейное однородное рекуррентное соотношение с постоянными коэффициентами , начальные значения , .

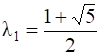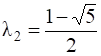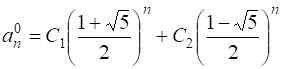Составим характеристическое уравнение и найдем характеристические числа и . Характеристическое уравнение имеет два различных корня кратности 1, значит, . Тогда общее решение , где и произвольные постоянные (, ). Используем заданные значения , составим систему из двух уравнений с двумя неизвестными:

Решением системы является пара чисел 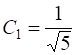и . Таким образом, .□

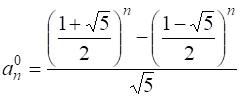Полученная формула называется формулой Бине и применяется для вычисления значений последовательности Фибоначчи только по их номеру, независимо от предыдущих членов последовательности.

Замечание. Часто рассматривается последовательность .

Например, для последовательности чисел Фибоначчи 0, 1, 1, 2, 3, 5, … рекуррентное соотношение записывается в виде , .

Задачи и упражнения.

13.1. Найдите формулу общего члена последовательности чисел, заданной рекуррентным соотношением , . Вычислите с помощью рекуррентного соотношения и по общей формуле.

13.2. Найдите формулу общего члена последовательности чисел, заданной рекуррентным соотношением , . Вычислите с помощью рекуррентного соотношения и по общей формуле.

13.3. Составьте рекуррентное соотношение последовательности квадратов натуральных чисел.

14. Понятие производящей функции.

Рассмотрим последовательность чисел

. (1)

Рассмотрим также последовательность функций действительной или комплексной переменной

. (2)

Формально составим функциональный ряд, используя элементы (1) и (2):

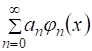. (3)

Будем считать ряд (3) сходящимся абсолютно на Или в некоторой области комплексной плоскости. Функция 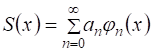Является суммой ряда (3).

Определение. Сумма ряда (3) называется Производящей функцией для заданной последовательности чисел (1) по заданной последовательности функций (2).

Чаще других используются степенные функции Или 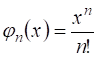. Поэтому ряд (3), как правило, является степенным.

Например. Положим в формуле бинома Ньютона . Тогда

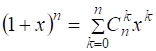. Значит, функция является производящей функцией для последовательности биномиальных коэффициентов по системе степенных функций .

Пример. Составить производящую функцию последовательности чисел Фибоначчи , , .

Решение. Используем последовательность функций действительной переменной Умножим рекуррентное соотношение на и просуммируем по :

. (4)

По допущению все ряды абсолютно сходятся на R.

.

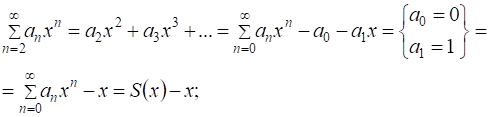
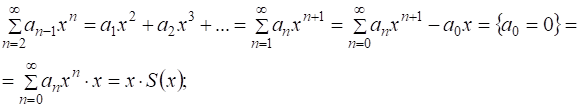
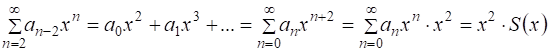Подставив суммы в (4), получим , тогда .□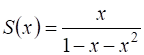

Задачи и упражнения.

14.1. Докажите, что функция является производящей для последовательности числе, общий член которой имеет вид .

14.2. Найдите производящую функцию для последовательности чисел .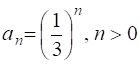

14.3. Найдите общий член последовательности, для которой функция 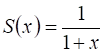является производящей.

14.4. Найдите общий член последовательности, для которой функция является производящей.

< Предыдущая