09. Подстановки множества
Рассмотрим конечное непустое множество ![]() ,
, ![]() .
.
Определение. Подстановкой ![]() -й степени множества
-й степени множества ![]() называется взаимно однозначное отображение
называется взаимно однозначное отображение ![]() множества
множества ![]() на себя
на себя
![]() .
.
Если каждому элементу множества ставится в соответствие его номер – натуральное число, не превосходящее ![]() , то подстановка множества записывается в виде матрицы размерности
, то подстановка множества записывается в виде матрицы размерности ![]() :
:
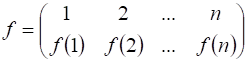 .
.
Элементы первой строки матрицы являются прообразами отображения ![]() , элементы второй строки матрицы являются образами отображения
, элементы второй строки матрицы являются образами отображения ![]() .
.
Определение. Канонической называется подстановка, в которой прообразы располагаются в порядке возрастания.
Множество всех различных подстановок данного множества ![]() мощности N обозначается
мощности N обозначается ![]() . Мощность множества
. Мощность множества ![]() равна числу перестановок элементов множества A.
равна числу перестановок элементов множества A.
![]() .
.
Например, для заданного множества ![]() число всех его подстановок равно
число всех его подстановок равно ![]() . Подстановки
. Подстановки  и
и  являются различными каноническими подстановками множества
являются различными каноническими подстановками множества ![]() . Подстановка
. Подстановка 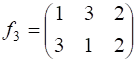 не является канонической.
не является канонической.
Определение. Произведением двух подстановок ![]() и
и ![]() множества А называется композиция
множества А называется композиция ![]() отображений
отображений ![]() и
и ![]() .
.
Например, произведение подстановок 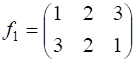 и
и 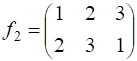 равно
равно
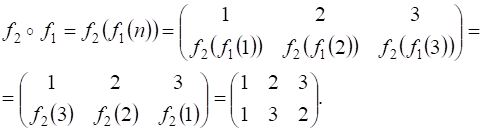
Произведение подстановок 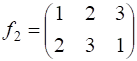 и
и  равно:
равно:
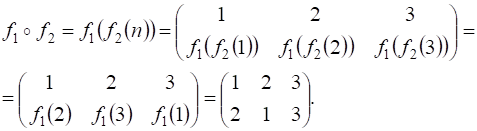
Произведение подстановок множества не является коммутативным.
Теорема 9.1. Для любых трех подстановок множества А ![]() ,
, ![]() и
и ![]() верно
верно ![]() .
.
Рассмотрим множество ![]() ,
, ![]() .
.
Определение. Тождественной Подстановкой ![]() -й степени называется взаимно однозначное отображение
-й степени называется взаимно однозначное отображение ![]() множества
множества ![]() на себя
на себя
![]() .
.
В матричной форме тождественная подстановка записывается  .
.
Определение. Обратной подстановкой множества А называется подстановка ![]() , удовлетворяющая условиям
, удовлетворяющая условиям ![]() .
.
Теорема 9.2. Для любой подстановки ![]() множества А существует единственная обратная подстановка
множества А существует единственная обратная подстановка ![]() .
.
Теорема 9.3.
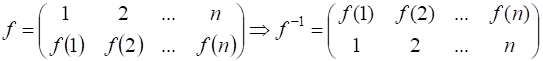 .
.
Например, для подстановки 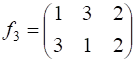 множества
множества ![]() обратная подстановка
обратная подстановка 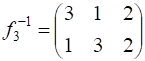 .
.
В комбинаторном анализе под Инверсией понимается пара образов ![]() подстановки множества, в которой
подстановки множества, в которой ![]() при
при ![]() .
.
Также Инверсией называется перемена местами двух соседних образов Канонической подстановки.
Теорема 9.4. Всякую подстановку ![]() можно представить в виде произведения инверсий.
можно представить в виде произведения инверсий.
Обозначим ![]() число инверсий, приводящих данную подстановку к тождественной подстановке.
число инверсий, приводящих данную подстановку к тождественной подстановке.
Определение. Число ![]() называется Чётностью подстановки
называется Чётностью подстановки ![]() .
.
Определение. Чётной называется подстановка ![]() , для которой
, для которой ![]() , Нечётной называется подстановка
, Нечётной называется подстановка ![]() , для которой
, для которой ![]() .
.
Например, каноническая подстановка 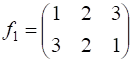 множества
множества ![]() является нечётной, так как число инверсий, приводящих
является нечётной, так как число инверсий, приводящих ![]() к
к ![]() равно трём:
равно трём:
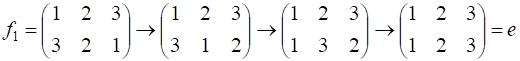 .
.
В множестве ![]() имеется
имеется ![]() чётных и
чётных и ![]() нечётных подстановок.
нечётных подстановок.
Задачи и упражнения.
9.1. Для следующих подстановок укажите степень подстановки, приведите подстановку к каноническому виду, найдите обратную подстановку:
1) 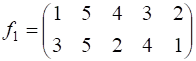 ; 2)
; 2) 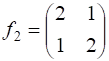 ;
;
3) 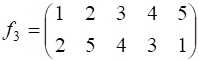 ; 4)
; 4) 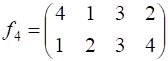 .
.
9.2. Для подстановок ![]() и
и ![]() задачи 3.21. найдите
задачи 3.21. найдите
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
9.3. Найти чётность подстановки ![]() для заданных подстановок
для заданных подстановок  и
и  .
.
| < Предыдущая | Следующая > |
|---|