07. Сочетания
Рассмотрим непустое конечное множество 
, 
.
1.) Из 
элементов этого множества сформируем различные выборки Без возвращения и без учёта порядка извлечённых элементов. Получаемые при таких условиях выборки называются Сочетаниями из 
элементов по элементов.
Число сочетаний для данного множества обозначается 
и вычисляется по формуле
.
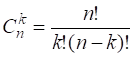Пример. Для проведения устного экзамена по математике создается комиссия из двух человек. Сколько различных комиссий можно организовать из 5 преподавателей?
Решение. Обозначим символом 
множество преподавателей, 
. Для ответа на вопрос задачи требуется найти число неупорядоченных выборок без повторений из 5 элементов (число преподавателей) по 2 элементов (число членов комиссии):
.□
2) Из элементов множества А сформируем различные выборки С возвращением и без учёта порядка извлечённых элементов. Получаемые при таких условиях выборки называются Сочетаниями с повторениями Из 
элементов по элементов. Возможно, что больше .
Число сочетаний с повторениями для данного множества обозначается 
и вычисляется по формуле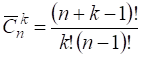 
.
Пример. В магазине продаются мячи синего, красного и зеленого цветов. Сколькими способами можно купить два мяча в этом магазине?
Решение. Обозначим символом множество цветов мячей, 
. Для ответа на вопрос задачи требуется найти число неупорядоченных выборок с повторениями из 3 элементов (число цветов мячей) по 2 элементов (число приобретаемых мячей):
.□
Задачи и упражнения.
7.1. В группе из 18 человек, среди которых есть студент N, выбирают 5 делегатов конференции. Сколькими способами можно сделать такой выбор? В скольких случаях в число делегатов попадет студент N?.
7.2. Сколько хорд можно провести через 6 точек, лежащих на одной окружности?
7.3. В почтовом отделении продаются открытки десяти видов. Сколькими способами можно купить здесь набор из семи открыток, если открыток каждого вида имеется не менее семи штук?
7.4. В магазине имеется 6 сортов шоколадных конфет и 4 сорта карамели. Сколько можно сделать различных покупок, содержащих два сорта карамели два сорта шоколадных конфет?
7.5. В кондитерском магазине продаются пирожные десяти видов. Сколькими способами можно купить здесь пять пирожных, если пирожных каждого вида имеется не менее пяти штук?
7.6. Сколько получится различных параллелограммов при пересечении четырех параллельных линий пятью другими параллельными линиями?
7.7. Докажите, что 
.
8. Виды основных комбинаторных конфигураций.
В сложных комбинаторных задачах совмещаются различные комбинаторные схемы. В таблице 1 приведены формулы для вычисления числа основных комбинаторных конфигураций, определённых в пунктах 5-7.
Таблица 1.
Основные комбинаторные формулы
Задачи и упражнения.
8.1. Решите систему уравнений
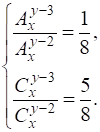
8.2. Сколькими способами можно переставить буквы слова «перешеек» так, чтобы две буквы «е» не шли подряд?
8.3. Сколько существует способов поставить Иванова, Петрова и еще 6 человек в очередь друг за другом так, чтобы между Ивановым и Петровым стояли 3 человека?
| < Предыдущая | Следующая > |
|---|
