3. Тренинг и задания по формированию компетенций
1 Алгоритм формирования компетенций
|
Компетенция |
Этап формирования*. Алгоритм расчета |
|
Освоения методики использо-вания программных средств для решения практических задач (ПК-2) |
А. Вычислить линейную комбинацию двух векторов, заданных своими координатами 1. Изучить определение и свойства сложения и вычитания двух векторов, заданных своими координатами. 2. Изучить определение и свойства умножения вектора на число. 3. Изучить определение и свойства линейной комбинации векторов 4. Вычислить вектор 5. Вычислить вектор 6. Сложив полученные векторы, получить искомую линейную комбинацию |
|
В. Вычислить скалярное произведение двух векторов, заданных своими координатами 1. Изучить определение и свойства скалярного произведения двух векторов, заданных своими координатами 2. Вычислить скалярное произведение по формуле | |
|
С. Вычислить площадь треугольника, построенного на векторах 1. Изучить определение и свойства векторного произведения 2. Найти координаты векторного произведения 3. Вычислить модуль векторного произведения 4. Выписать ответ: площадь треугольника S равна половине площади параллелограмма, т. е. S = |
|
D. Проверить, будут ли векторы 1. Изучить определение смешанного произведения трех векторов, его вычисление через координаты сомножителей и геометрический смысл. 2. Вычислить смешанное произведение 3. Сделать вывод: если | |
|
E. Вычислить определитель третьего порядка, разложив его по элементам 1. Изучить определение определителя третьего порядка и способы его вычисления. 2. Вычислить алгебраические дополнения элементов 3. Вычислить определитель по формуле Det А= |
2 Формирование компетенций
ПК-2. Освоение методики использования программных средств для решения практических задач
Этап формирования ПК-2. А. Вычислить линейную комбинацию двух векторов, заданных своими координатами ![]() (
(![]() Заданные действительные числа)
Заданные действительные числа)
Решение типовой задачи
Условие задачи
Вычислить линейную комбинацию ![]() двух векторов
двух векторов ![]() {–1, 2, 3} и
{–1, 2, 3} и ![]() {2, 0, 1}. заданных своими координатами.
{2, 0, 1}. заданных своими координатами.
Решение задачи
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
Ознакомиться с определением линейной комбинации векторов, заданных своими координатами |
|
|
2 |
Вычислить вектор |
В данном случае вектор |
|
3 |
Вычислить вектор |
В данном случае вектор |
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
4 |
Сложить полученные векторы и получить |
В данном случае
|
|
5 |
Выписать ответ |
Линейной комбинацией двух исходных векторов будет вектор |
Задачи для самостоятельной работы
Задача 1
Даны векторы ![]() ={1, 0, –2} и
={1, 0, –2} и ![]() ={3, –1, 1}. Найти линейную комбинацию этих векторов
={3, –1, 1}. Найти линейную комбинацию этих векторов
![]() .
.
Задача 2
Даны векторы ![]() ={7, 0, –3} и
={7, 0, –3} и ![]() ={0, –1, 1}. Найти линейную комбинацию этих векторов
={0, –1, 1}. Найти линейную комбинацию этих векторов
![]() .
.
Задача 3
Даны векторы ![]() ={0, 0, –3} и
={0, 0, –3} и ![]() ={0, –1, 1}. Найти линейную комбинацию этих векторов
={0, –1, 1}. Найти линейную комбинацию этих векторов
![]() .
.
Задача 4
Даны векторы ![]() ={3, 0, –3} и
={3, 0, –3} и ![]() ={0, –1, 6}. Найти линейную комбинацию этих векторов
={0, –1, 6}. Найти линейную комбинацию этих векторов
![]() .
.
Задача 5
Даны векторы ![]() ={7, 0, –4} и
={7, 0, –4} и ![]() ={0, –1, 0}. Найти линейную комбинацию этих векторов
={0, –1, 0}. Найти линейную комбинацию этих векторов
![]() .
.
Этап формирования ПК-2. В. Вычислить скалярное произведение двух векторов, заданных своими координатами ![]() и
и ![]()
Решение типовой задачи
Условие задачи
Вычислить скалярное произведение двух векторов ![]() и
и ![]() , если векторы
, если векторы ![]() заданы своими координатами:
заданы своими координатами: ![]() {–1, 2, 3} и
{–1, 2, 3} и ![]() {2, 0, 1}
{2, 0, 1}
Решение задачи
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
Ознакомиться с определением скалярного произведения векто-ров, заданных своими коорди-натами |
Общая формула скалярного произведения имеет вид |
|
2 |
Вычислить вектор |
В данном случае вектор |
|
3 |
Вычислить вектор |
В данном случае вектор
|
|
4 |
Вычислить скалярное произведение двух полученных векторов |
В данном случае
|
|
5 |
Выписать ответ |
|
Задачи для самостоятельной работы
Задача 1
Даны векторы ![]() ={0, 0, –2} и
={0, 0, –2} и ![]() ={3,0, 1}. Найти скалярное произведение векторов,
={3,0, 1}. Найти скалярное произведение векторов,
![]() и
и ![]() .
.
Задача 2
Даны векторы ![]() ={3, 2, –2} и
={3, 2, –2} и ![]() ={0,0, 1}. Найти скалярное произведение векторов,
={0,0, 1}. Найти скалярное произведение векторов,
![]() и
и ![]() .
.
Задача 3
Даны векторы ![]() ={8, 3, –2} и
={8, 3, –2} и ![]() ={1,1, 1}. Найти скалярное произведение векторов,
={1,1, 1}. Найти скалярное произведение векторов,
![]() и
и ![]() .
.
Задача 4
Даны векторы ![]() ={15, -3, –2} и
={15, -3, –2} и ![]() ={0,2, 1}. Найти скалярное произведение векторов,
={0,2, 1}. Найти скалярное произведение векторов,
![]() и
и ![]() .
.
Задача 5
Даны векторы ![]() ={1, 2, –3} и
={1, 2, –3} и ![]() ={5,0, 1}. Найти скалярное произведение векторов,
={5,0, 1}. Найти скалярное произведение векторов,
![]() и
и ![]() .
.
Этап формирования ПК-2. С. Вычислить площадь треугольника, построенного на векторах ![]() и
и ![]()
Решение типовой задачи
Условие задачи
Найти площадь треугольника SD, построенного на векторах ![]() {–1, 2, 3} и
{–1, 2, 3} и ![]() {2, 0, 1}.
{2, 0, 1}.
Решение задачи
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
Ознакомиться с определением вектора, равного векторному произведению |
|
|
2 |
Вычислить координаты векторного произведения
|
|
|
3 |
Вычислить модуль векторного произведения |
|
|
4 |
Выписать ответ |
Площадь
|
Задачи для самостоятельной работы
Задача 1
Даны векторы ![]() ={1, 0, –2} и
={1, 0, –2} и ![]() ={3, –1, 1}. Найти векторное произведение векторов
={3, –1, 1}. Найти векторное произведение векторов ![]() и
и ![]() , где
, где ![]() =
= ![]() +
+ ![]() ,
, ![]() = 2
= 2![]() –
– ![]() .
.
Задача 2
Найти площадь параллелограмма, построенного на векторах ![]() +
+ ![]() и
и ![]() –
– ![]() , где
, где ![]() ={1, 1, –1},
={1, 1, –1}, ![]() ={2, 0, 3}.
={2, 0, 3}.
Задача 3
Найти векторы ![]() , где
, где ![]() – базисная тройка.
– базисная тройка.
Задача 4
Найти координаты вектора ![]() , если известно:
, если известно:
1) ![]() ^
^![]() ,
, ![]() = {–1, 1, 0};
= {–1, 1, 0};
2) ![]() ^
^![]() ,
, ![]() = {0, 3, 2};
= {0, 3, 2};
3) |![]() |2 = 68.
|2 = 68.
Задача 5
Найти площадь параллелограмма, построенного на векторах ![]() =
= ![]() + 2
+ 2![]() ,
, ![]() = 2
= 2![]() +
+ ![]() , как на сторонах, если
, как на сторонах, если ![]() и
и ![]() – единичные векторы, угол между которыми равен 30°.
– единичные векторы, угол между которыми равен 30°.
Этап формирования ПК-2. D. Проверить, будут ли векторы ![]() = {X1, Y1, Z1},
= {X1, Y1, Z1}, ![]() = {X1, Y1, Z1},
= {X1, Y1, Z1},
![]() = {X3, Y3, Z3} линейно зависимы (компланарны). В противном случае найти объем параллелепипеда, построенного на этих векторах
= {X3, Y3, Z3} линейно зависимы (компланарны). В противном случае найти объем параллелепипеда, построенного на этих векторах
Решение типовой задачи
Условие задачи
Проверить, будут ли векторы ![]() ={1, 2, 1},
={1, 2, 1}, ![]() ={2, –6, 3} и
={2, –6, 3} и ![]() ={0, 2, –1} компланарны и найти объем параллелепипеда, построенного на
={0, 2, –1} компланарны и найти объем параллелепипеда, построенного на ![]() ,
, ![]() ,
, ![]() в противном случае.
в противном случае.
Решение
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
Изучить определение сме-шанного произведения трех векторов, его вычисление через координаты сомно-жителей и геометрический смысл | |
|
2 |
Вычислить смешанное произ-ведение |
Определитель считаем разложением по 1-му столбцу |
|
3 |
Сделать вывод: если |
Так как |
Задачи для самостоятельной работы
Задача 1
Вычислить объем тетраэдра, построенного на векторах ![]() ,
, ![]() и
и ![]() как на сторонах, если
как на сторонах, если
![]() ={4, –1, 2},
={4, –1, 2}, ![]() ={0, –1, 0},
={0, –1, 0}, ![]() ={2, 1, –3}.
={2, 1, –3}.
Задача 2
Найти высоту параллелепипеда, построенного на векторах ![]() ={1, 1, 1},
={1, 1, 1}, ![]() ={2, 0, –1},
={2, 0, –1},
![]() ={0, 3, –1}.
={0, 3, –1}.
Задача 3
Найти объем параллелепипеда, построенного на векторах ![]() ,
, ![]() ,
, ![]() , если известно, что
, если известно, что
![]() ={1, 3, –5},
={1, 3, –5}, ![]() ={0, 2, 5}, скалярные произведения (
={0, 2, 5}, скалярные произведения (![]() ,
,![]() ) = 0, (
) = 0, (![]() ,
,![]() ) = 1 и вектор
) = 1 и вектор ![]() перпендикулярен оси ОХ.
перпендикулярен оси ОХ.
Задача 4
Доказать, что четыре точки А(1, 2, –1), В(0, 1, 5), С(–1, 2, 1), D(2, 1 ,3) лежат в одной плоскости.
Задача 5
Вектор ![]() ортогонален векторам
ортогонален векторам ![]() и
и ![]() ; |
; |![]() | = 3, |
| = 3, |![]() | = 5, |
| = 5, |![]() | = 2; угол между векторами
| = 2; угол между векторами ![]() и
и ![]() равен
равен ![]() , т. е. (
, т. е. (![]() Ù
Ù ![]() ) =
) = ![]() . Вычислить
. Вычислить ![]() ,
, ![]() ,
, ![]() .
.
Задача 6
Определить, какой является тройка векторов![]() ,
, ![]() ,
, ![]() (левой или правой), если
(левой или правой), если
![]() =
= ![]() ,
, ![]() = =
= = ![]() ,
, ![]() =
= ![]() .
.
Этап формирования ПК-2. Е. Вычислить определитель третьего порядка, разложив его по элементам I-ой строки (или столбца)
Решение типовой задачи
Условие задачи
Вычислить определитель третьего порядка, разложив его по элементам первой строки
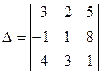 .
.
Решение задачи
|
№ П/п |
Этап (шаг) алгоритма |
Конкретное действие в соответствии |
|
1 |
Изучить определение определителя третьего порядка и способы его вычисления |
В данном случае задан определитель третьего порядка |
|
|
Вычислить алгебраические дополнения элементов первой строки |
Вычислим алгебраические дополнения элементов первой строки. Для Для Для |
|
3 |
Определитель считаем разложением по 1-му столбцу |
В нашем случае получим
|
Задачи для самостоятельной работы
Задача 1
Вычислить определитель 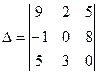 , разложив его по элементам второй строки.
, разложив его по элементам второй строки.
Задача 2
Вычислить определитель 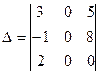 , разложив его по элементам третьей строки.
, разложив его по элементам третьей строки.
Задача 3
Вычислить определитель 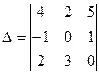 , разложив его по элементам второго столбца.
, разложив его по элементам второго столбца.
Задача 4
Вычислить определитель 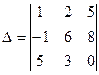 , разложив его по элементам первого столбца.
, разложив его по элементам первого столбца.
Задача 5
Вычислить определитель 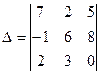 , разложив его по элементам третьего столбца.
, разложив его по элементам третьего столбца.
| < Предыдущая | Следующая > |
|---|
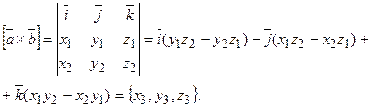
 .
.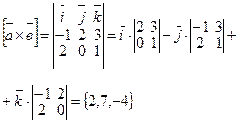
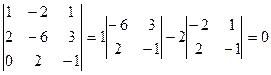 .
.