2.9 Угол между векторами

Найдем угол между ненулевыми векторами {X1, Y1, Z1} и {X2, Y2, Z2}.

Возьмем скалярное произведение и Определим косинус угла J между этими векторами:

(2.25)

Если же векторы и перпендикулярны, то и, следовательно,

. (2.26)

Это равенство является Условием ортогональности (перпендикулярности) двух векторов.

Приведем несколько примеров на использование рассмотренных формул.

Пример. Найти угол между векторами {1, 1, 1} и {2, 0, 3}.

Решение

.

Откуда 36°50'.

Пример. Вершины треугольника АВС имеют координаты А(1, 2, –3); В(0, 1, 2); С(2, 1 ,1). Найти длины сторон АВ и АС И угол при вершине А.

Решение

Чтобы найти координаты вектора, следует из координат точки–конца вектора вычесть координаты точки–начала.

.

.

.

.

.

Пример. Найти проекцию вектора {5, –3, 7} на вектор {2, –2, 1}.

Решение.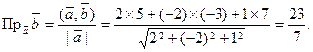

< Предыдущая		Следующая >