2. Элементы векторной алгебры. 2.1 Скалярные и векторные величины

Величины, встречающиеся в механике, физике и других прикладных науках, могут быть разделены на две категории. С одной стороны, это величины, которые определяются только числовым значением (числом), например масса, температура тела, объем; с другой – величины, для определения которых необходимо знать не только числовое значение, но и направление, например сила, скорость, ускорение. Величины первого типа называются Скалярными величинами, величины второго типа – Векторными величинами.

Скалярная величина может быть задана числом в выбранной системе единиц. Векторную величину можно задать в виде направленного отрезка, предварительно выбрав линейный масштаб. Вектор, началом которого служит точка А, а концом – точка В, обозначается (рисунок 1). Вектор обозначается также одной буквой, как показано на рисунке 2. Эту букву печатают жирным шрифтом, а в письме ставят над буквой черту. Длина вектора называется модулем и обозначается двумя вертикальными чертами справа и слева: || или ||.

Рисунок 1 Рисунок 2

Вектор , начало и конец которого совпадают, называется нулевым вектором. Его модуль равен нулю. Нулевой вектор не имеет определенного направления.

Векторы, лежащие на параллельных прямых (или на одной и той же прямой), называются Коллинеарными.

Векторы на рисунке 3 коллинеарные.

Рисунок 3

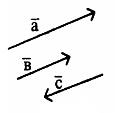
Коллинеарные векторы могут иметь одно и то же направление (равнонаправленные векторы) или противоположное. Так, векторы и (см. рисунок 3) равнонаправлены, векторы и (также и ) противоположно направлены.

Нуль-вектор считается коллинеарным любому вектору.

Два (ненулевых) вектора И Равны, если они равнонаправлены и имеют один и тот же модуль.

Так, векторы и на рисунке 4 равны, а векторы и не равны.

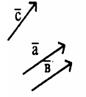
Рисунок 4

Это записывается так: = , ¹ .

Два вектора, имеющие равные модули и противоположно направленные, называются Противоположными. Вектор, противоположный вектору , обозначается –.

Так, векторы и на рисунке 5 противоположные. Из определения следует, что – , .

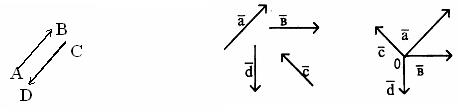
Рисунок 5 Рисунок 6

Всякие векторы (в любом числе) можно привести к общему началу, т. е. построить векторы, соответственно равные данным и имеющие общее начало в точке 0. Такое приведение изображено на рисунке 6.

Итак, в дальнейшем будем иметь дело со свободными векторами, т. е. векторами, определенными с точностью до параллельного переноса.

< Предыдущая		Следующая >