1.5 Правило Крамера
Рассмотрим для начала случай одного уравнения первой степени с одним неизвестным
![]() .
.
При решении этого уравнения возможны три случая:
1. Если ![]() , то уравнение имеет единственное решение
, то уравнение имеет единственное решение ![]() .
.
2. Если ![]() , то уравнение имеет бесчисленное множество решений. Действительно, любое действительное число
, то уравнение имеет бесчисленное множество решений. Действительно, любое действительное число ![]() является решением, так как
является решением, так как ![]() .
.
3. Если ![]() , то уравнение не имеет решений.
, то уравнение не имеет решений.
Такие же три случая возможны и при решении произвольной системы линейных уравнений, в чем мы убедимся в курсе алгебры в одной из последующих юнит. Рассмотрим теперь формулы Крамера, которые позволяют найти решение систем линейных уравнений через отношения соответствующих определителей.
Рассмотрим систему двух линейных уравнений с двумя неизвестными
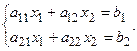 (1.9)
(1.9)
Матрица коэффициентов при неизвестных

Называется матрицей системы; вектор ![]() – вектором правых частей, а
– вектором правых частей, а ![]() – вектором неизвестных системы.
– вектором неизвестных системы.
Найти решение системы, это значит найти числа X1, X2, удовлетворяющие уравнениям системы. Умножим первое уравнение системы на A22, а второе – на A12 и вычтем из первого уравнения второе. В результате коэффициент при X2 станет равным нулю, и мы получим формулу для вычисления неизвестной величины X1
(A11A22 – A21A12)X1 = (B1A22 – B2A12). (1.10)
Видно, что коэффициент при X1 является определителем матрицы А:

А в правой части равенства стоит определитель, полученный из матрицы А заменой первого столбца вектором правых частей; обозначим его
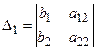 .
.
Уравнение (1.10) можно теперь записать так:
D × X1 = D1.
Пусть D ¹ 0, тогда
![]() (1.11)
(1.11)
Аналогично можно показать, что
![]() (1.12)
(1.12)
Здесь  , то есть определитель D2 получен из определителя D путем замены второго столбца вектором правых частей. Формулы (1.11) и (1.12) называют правилом Крамера.
, то есть определитель D2 получен из определителя D путем замены второго столбца вектором правых частей. Формулы (1.11) и (1.12) называют правилом Крамера.
Итак, справедлива теорема. Если определитель системы отличен от нуля, то система имеет единственное решение, которое находится по правилу Крамера.
Правило Крамера верно для произвольной системы N уравнений с N неизвестными. Формулы в этом случае имеют вид:
![]() (1.13)
(1.13)
Здесь D – определитель матрицы системы, а DI – определитель, полученный из D путем замены I-го столбца на столбец (вектор) правых частей.
| < Предыдущая | Следующая > |
|---|