2.10 Векторное произведение
В предыдущих разделах мы рассматривали скалярное произведение двух векторов. Однако существуют и другие способы определения произведения векторов. В частности, можно ввести понятия векторного и смешанного произведения двух векторов. Рассмотрим эти понятия.
Определение. Векторным произведением двух векторов 
и 
называется вектор 
, удовлетворяющий следующим условиям:
1) || = || × || × sin j, где j – угол между векторами и ;
2) ^ и ^, т. е. вектор перпендикулярен плоскости "натянутой" на векторы и ;
3) векторы , и (после приведения к общему началу) ориентированы по отношению друг к другу, соответственно, как орты 
, 
и 
, т. е. образуют так называемую "правую" тройку векторов.
Векторное произведение на обозначается так: ´ или [ ´ ].
Свойства векторного произведения
1. 
, т. е. векторное произведение не обладает переместительным свойством, то есть при перестановке сомножителей векторное произведение меняет направление;
2. ´ = 
, если = или = , либо || .
3. ´(+) = ´ + ´ (распределительное свойство).
4. l´ = ´l = l[´] (сочетательное свойство по отношению к скалярному множителю).
5. (a + b) ´ = a[´] + b[´] (линейность по первой компоненте).
Аналогично, справедлива линейность и по второй компоненте.
Модуль векторного произведения = ´ численно равен площади параллелограмма, построенного на векторах и (рисунок 15).
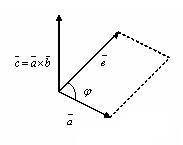
Рисунок 15
В Координатной форме векторное произведение векторов = {X1, Y1, Z1} и = {X2, Y2, Z2} вычисляется следующим образом:
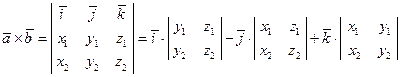. (2.27)
Правая часть этой формулы получена разложением определителя третьего порядка по элементам первой строки, в которой стоят орты прямоугольной трехмерной системы координат.
Из формулы следует, что координатами векторного произведения служат определители:
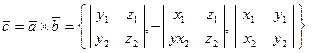. (2.28)
Заметим, что определитель, применяемый в формуле (2.27) для вычисления векторного произведения, отличается от рассмотренных ранее, так как в первой его строке находятся не числа, а орты , , . Но такой способ записи удобен, и мы будем пользоваться им, причем разложение следует делать по первой строке.
Пример. Вычислить площадь параллелограмма, построенного на векторах {4, 1, 3} и
= {2, 1, 0}.
Площадь искомого параллелограмма равна модулю вектора = ´ . Найдем координаты этого вектора:
.
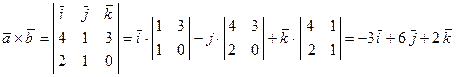Координаты вектора = ´ = {–3, 6, 2}.
Теперь вычислим модуль этого вектора
Ответ: площадь искомого параллелограмм равна S = 7 кв. ед.
| < Предыдущая | Следующая > |
|---|
