2.11 Смешанное произведение
Определение. Смешанным произведением трех векторов ![]() ,
, ![]() ,
, ![]() называется число, равное скалярному произведению вектора [
называется число, равное скалярному произведению вектора [![]() ´
´![]() ] на вектор
] на вектор ![]() , т. е. [
, т. е. [![]() ´
´![]() ] ×
] × ![]() .
.
Свойства смешанного произведения
1.Смешанное произведение трех векторов равно нулю, если:
А) хоть один из перемножаемых векторов равен нулю;
Б) два из перемножаемых векторов коллинеарны;
В) все три вектора параллельны одной и той же плоскости (компланарны).
2. Смешанное произведение не изменится, если в нем поменять местами знаки векторного и скалярного умножения, т. е.
[![]() ´
´![]() ] ×·
] ×·![]() =
= ![]() × [
× [![]() ´
´![]() ].
].
В силу этого свойства смешанное произведение векторов ![]() ,
, ![]() и
и ![]() принято записывать так:
принято записывать так: ![]() . Можно показать, что Смешанное произведение трех векторов
. Можно показать, что Смешанное произведение трех векторов ![]() ,
, ![]() ,
,![]() По модулю равно объему параллелепипеда, построенного на этих векторах. В этом состоит геометрический смысл смешанного произведения и определителя третьего порядка (рисунок 16).
По модулю равно объему параллелепипеда, построенного на этих векторах. В этом состоит геометрический смысл смешанного произведения и определителя третьего порядка (рисунок 16).
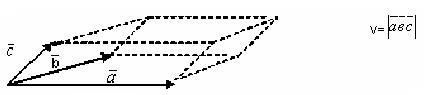
Рисунок 16
Объем V1 треугольной пирамиды, построенной на векторах ![]() ,
, ![]() ,
, ![]() , вычисляется по формуле V1 =
, вычисляется по формуле V1 = ![]() .
.
Из свойств смешанного произведения вытекает следующее: необходимым и достаточным Условием компланарности трех векторов служит условие равенства нулю их смешанного произведения ![]() = 0 (объем параллелепипеда равен нулю).
= 0 (объем параллелепипеда равен нулю).
Пусть векторы заданы своими координатами ![]() ={A1, A2, A3},
={A1, A2, A3}, ![]() = {B1, B2, B3},
= {B1, B2, B3}, ![]() = {C1, C2, C3}.
= {C1, C2, C3}.
Тогда их Смешанное произведение можно Вычислить по формуле
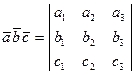 (2.29)
(2.29)
Таким образом, если три вектора лежат в одной плоскости, то
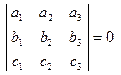 (2.30)
(2.30)
Итак, в случае компланарности векторов один из векторов линейно выражается через другие, то есть векторы ![]() ,
, ![]() ,
, ![]() линейно зависимы.
линейно зависимы.
Отсюда следует свойство определителя: если строки (столбцы) определителя линейно зависимы, то определитель равен нулю.
Замечание
Если векторы ![]() ,
, ![]() ,
, ![]() образуют правую тройку, то их смешанное произведение положительно:
образуют правую тройку, то их смешанное произведение положительно: ![]() > 0 означает, что эти векторы образуют правую тройку.
> 0 означает, что эти векторы образуют правую тройку.
Если же ![]() < 0, то векторы образуют левую тройку (и обратно).
< 0, то векторы образуют левую тройку (и обратно).
| < Предыдущая | Следующая > |
|---|