2.12 Понятие арифметического n-мерного пространства
В предыдущих параграфах мы рассмотрели векторы в декартовой прямоугольной системе координат с базисом ![]() ,
, ![]() ,
, ![]() . Мы знаем теперь, что любой вектор
. Мы знаем теперь, что любой вектор ![]() в этой системе можно разложить по базису, т. е. представить в виде
в этой системе можно разложить по базису, т. е. представить в виде
![]() ,
,
Где числа X, Y, Z являются координатами вектора ![]() в базисе
в базисе ![]() ,
, ![]() ,
, ![]() , и однозначно его определяют. Итак, можно считать вектором
, и однозначно его определяют. Итак, можно считать вектором ![]() упорядоченную тройку чисел (X, Y, Z).
упорядоченную тройку чисел (X, Y, Z).
Например, вектор ![]() представляет тройка чисел (1, 0, 0), соответственно,
представляет тройка чисел (1, 0, 0), соответственно, ![]() – {0, 1, 0},
– {0, 1, 0}, ![]() – {0, 0, 1}.
– {0, 0, 1}.
Будем говорить, что эти векторы заданы в трехмерном пространстве R3 (3 – размерность пространства). Векторы ![]() ,
, ![]() ,
, ![]() образуют базис пространства R3.
образуют базис пространства R3.
Можно теперь обобщить введенные понятия. Назовем Вектором N-мерного пространства Rn упорядоченную совокупность N чисел {X1, X2,…, Xn}. Особые векторы
![]() {1, 0, 0,..., 0},
{1, 0, 0,..., 0}, ![]() {0, 1, 0,..., 0}, ...,
{0, 1, 0,..., 0}, ..., ![]() {0, 0, 0, ..., 1}
{0, 0, 0, ..., 1}
Образуют Канонический базис пространства RN.
Многие понятия, относящиеся к RN, взяты из трехмерного пространства. Подобно тому, как это было сделано ранее, можно операции над векторами в пространстве RN свести к операциям над их координатами.
Пусть ![]() ={A1, A2,..., An},
={A1, A2,..., An}, ![]() = {B1, B2,..., Bn} – два вектора пространства RN.
= {B1, B2,..., Bn} – два вектора пространства RN.
1. Суммой векторов ![]() ,
,![]() называется вектор
называется вектор ![]() =
= ![]() +
+ ![]() , координаты которого равны суммам соответствующих координат векторов
, координаты которого равны суммам соответствующих координат векторов ![]() и
и ![]() , т. е.
, т. е.
![]() = {C1, C2, ..., Cn}, где
= {C1, C2, ..., Cn}, где ![]() (I =
(I = ![]() ). (2.31)
). (2.31)
2. Произведением вектора ![]() на число λ называется вектор, координаты которого равны произведению соответствующих координат вектора
на число λ называется вектор, координаты которого равны произведению соответствующих координат вектора ![]() на число λ:
на число λ:
l![]() = {lA1, lA2, …, lN}. (2.32)
= {lA1, lA2, …, lN}. (2.32)
Вектор ![]() называется нулевым вектором.
называется нулевым вектором.
Вектор ![]() называется Линейной комбинацией векторов
называется Линейной комбинацией векторов ![]() с коэффициентами
с коэффициентами ![]() . Векторы
. Векторы ![]() называются Линейно зависимыми, если существуют такие числа
называются Линейно зависимыми, если существуют такие числа ![]() , не равные нулю одновременно, что
, не равные нулю одновременно, что ![]() .
.
Если же это равенство выполняется лишь при l1 = l2 = ... = lN = 0, то векторы ![]() называются Линейно независимыми. Можно показать, что векторы
называются Линейно независимыми. Можно показать, что векторы ![]() линейно независимы и любой вектор
линейно независимы и любой вектор ![]() можно представить в виде их линейной комбинации:
можно представить в виде их линейной комбинации:
![]() (2.33)
(2.33)
Это равенство представляет собой разложение вектора ![]() по базису
по базису ![]() . Числа
. Числа ![]() называются координатами вектора
называются координатами вектора ![]() в данном базисе. Координаты вектора по базису определяются однозначно.
в данном базисе. Координаты вектора по базису определяются однозначно.
Заметим, что любые N линейно независимых векторов из RN образуют базис пространства RN, Каждый вектор ![]() является однозначной линейной комбинацией векторов базиса. Координаты вектора зависят от базиса.
является однозначной линейной комбинацией векторов базиса. Координаты вектора зависят от базиса.
2. Скалярным произведением векторов ![]() и
и ![]() называется сумма произведений соответствующих компонент этих векторов, т. е.
называется сумма произведений соответствующих компонент этих векторов, т. е.
![]() . (2.34)
. (2.34)
По определению, модулем вектора |![]() | называется величина
| называется величина
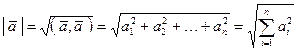 . (2.35)
. (2.35)
Угол между двумя векторами можно определить по следующей формуле:
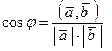 , (2.36)
, (2.36)
Или
 (2.37)
(2.37)
Можно показать, что ![]() и
и ![]() .
.
Как и ранее, условием ортогональности двух векторов служит равенство
(![]() ) = 0 или A1B1 + A2B2 + … + Anbn = 0. (2.38)
) = 0 или A1B1 + A2B2 + … + Anbn = 0. (2.38)
| < Предыдущая | Следующая > |
|---|